Prime Factorization

Prime factorization is one of the fundamental concepts in arithmetic and number theory. It helps in breaking down a number into a product of its prime numbers. Understanding what is prime factorization and how to find prime factorization is essential for solving many mathematical problems, such as calculating HCF, LCM, simplifying fractions, and working with large numbers in algebra and cryptography.

This guide explains the meaning of prime factorization, discusses the prime factors of a number, explores different prime factorization methods, and demonstrates everything with solved examples.

 

Table of Contents

• What is Prime Factorization?
• What are Prime Factors?
• Prime Factorization of a Number (1 to 30)
• Prime Factorization Methods
  • Division Method
  • Factor Tree Method
• Applications of Prime Factorization
• Solved Examples
• Conclusion
• FAQs on Prime Factorization

 

What is Prime Factorization?

To understand what is prime factorization, we first need to understand the concept of prime numbers. Prime numbers are the numbers that have only two factors, 1 and the number itself. Examples of prime numbers include 2, 3, 5, 7, 11, 13, and so on.

Prime factorization is the process of expressing a number as a product of prime numbers. These prime numbers are its prime factors. Each number has a unique prime factorization. For example, the prime factorization of 24 is 2 × 2 × 2 × 3, which can also be written as 2³ × 3. 

Simply put, if we decompose a number until we can no longer break it down except by using prime numbers, we get the prime factorization of that number.

 

What are Prime Factors?

Prime factorization is the process of expressing a number as a product of prime numbers. These prime numbers are called the prime factors of a number. Every number has a unique prime factorization. 

For example, the prime factorization of 24 is 2 × 2 × 2 × 3, which can also be written as 2³ × 3. 

In simple terms, if we keep breaking a number down until we can only use prime numbers, we get the prime factorization of that number.

 

Prime Factorization of a Number (1-30)

To make learning easier, the prime factorization of the first 30 natural numbers is presented in a table. For each number, you can see:

• Its prime factors, written as a product of primes.

• Its exponential form, where repeated prime factors are shown with powers.

For example, the number 12 can be expressed as 2 × 2 × 3, and in exponential form as 2² × 3¹. Similarly, 30 can be written as 2 × 3 × 5 or 2¹ × 3¹ × 5¹.

This table provides a quick reference to understand the prime factors of numbers from 1 to 30, making it easier for students to identify patterns and solve problems related to factors and multiples.

 

 

Prime Factorization Methods

There are two major ways to find the prime factorization of a number. Each prime factorisation method is systematic and helps in breaking down the number into its smallest components. Both methods help find the smallest prime numbers that multiply together to give the original number, making it easier to work with factors, multiples, HCF and LCM.

 

Division Method

The division method is a step-by-step way to find the prime factorization of a number by dividing it by the smallest prime number. You repeat this process with the resulting quotient until the final quotient is 1.

Here are the steps to follow using the division method:

1. Start by dividing the number by the smallest prime number, which is 2.

2. Keep dividing the result by the same prime number until it no longer divides evenly.

3. Move on to the next smallest prime number (3, 5, 7, etc.) and repeat the process.

4. Stop when the final quotient is 1.

This method works well for students who are comfortable with basic division and are handling small to moderately large numbers.

 

Example:

Find the prime factorization of 72.

Step 1: Divide 72 by the least prime number, which is 2.
72 ÷ 2 = 36

Step 2: Again divide 36 by 2.
36 ÷ 2 = 18

Step 3: Divide 18 by 2 again.
18 ÷ 2 = 9

Step 4: 2 no longer divides 9 evenly, so we move to the next smallest prime number, 3.
9 ÷ 3 = 3

Step 5: Divide 3 by 3.
3 ÷ 3 = 1

As we have reached 1, we stop.

So, the prime factors of 72 are 2 × 2 × 2 × 3 × 3, which can also be written in exponential form as 2³ × 3².

 

Factor Tree Method

The factor tree method is a visual way to find a number's prime factors. It works by dividing the number into two factors. You keep dividing the composite factors until all the resulting numbers are prime. 

Here are the steps to use the factor tree method:  

1. Write the number at the top of the tree.  

2. Break it into any two factors.  

3. If a factor is not a prime number, split it again into two factors.  

4. Keep going until all the branches end in prime numbers.  

The prime numbers at the end of the branches are the prime factors of the original number.

 

 

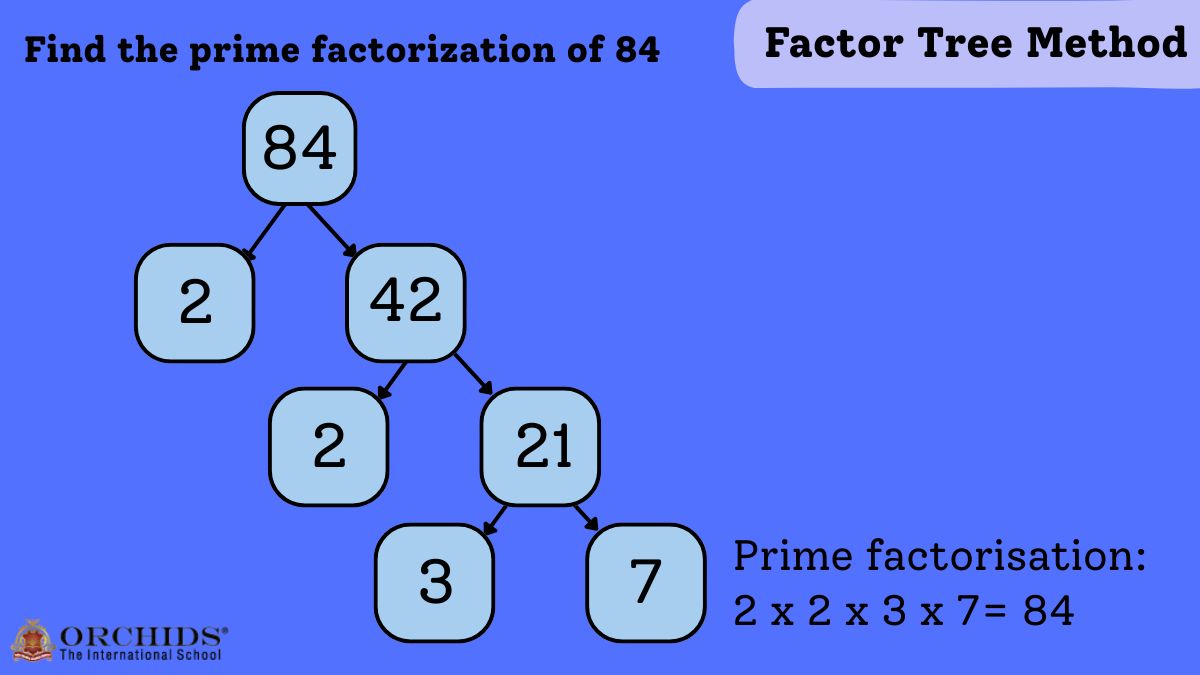
Both the division method and the factor tree method are reliable ways to understand how to find prime factorization. Choosing between them depends on whether you prefer a visual method or a procedural one.

 

Applications of Prime Factorization

Prime factorization is more than just a theoretical concept. It has several real-world and mathematical applications that make it a valuable tool in problem-solving.

• Finding the Highest Common Factor (HCF): To find the HCF of two or more numbers, prime factorization is used to identify common prime factors and select the lowest powers among them.

• Finding the Least Common Multiple (LCM): Prime factorization helps in finding the LCM by choosing the highest powers of all prime factors present in the numbers.

• Simplifying Fractions: Fractions can be simplified by canceling common prime factors from the numerator and the denominator.

• Algebraic Expressions: Many algebraic problems involving factorization and simplification benefit from expressing numbers in their prime factorized form.

• Cryptography: Modern encryption systems like RSA use very large numbers and their prime factorization as the basis for secure data encryption, making prime factorization essential in computer science and security.
  
  

Solved Examples

Let’s go through several examples that show how to find prime factorization using both methods.

Example 1: Prime Factorization of 100 

Step 1: Divide 100 by the least prime number, which is 2.
100 ÷ 2 = 50

Step 2: Divide 50 by 2 again.
50 ÷ 2 = 25

Step 3: Divide 25 by the next smallest prime number, 5.
25 ÷ 5 = 5

Step 4: Divide 5 by 5.
5 ÷ 5 = 1

As we have reached 1, we stop.

So, the prime factorization of 100 is 2 × 2 × 5 × 5, or in exponential form: 2² × 5².

 

Example 2: Prime Factorization of 126 

Step 1: Start with 126 at the top of the factor tree.
Step 2: Split 126 into two factors: 2 × 63

Step 3: Split 63 into 3 × 21

Step 4: Split 21 into 3 × 7

All the branches now end in prime numbers: 2, 3, 3, and 7.

So, the prime factorization of 126 is 2 × 3 × 3 × 7, or in exponential form: 2 × 3² × 7.

 

Example 3: Find HCF of 36 and 48 using Prime Factorization

Step 1: Find the prime factorization of each number.
36 = 2 × 2 × 3 × 3 = 2² × 3²
48 = 2 × 2 × 2 × 2 × 3 = 2⁴ × 3

Step 2: Identify the common prime factors.
Common prime factors are 2 and 3

Step 3: Take the lowest powers of the common primes.
Lowest power of 2 = 2²
Lowest power of 3 = 3¹

Step 4: Multiply these to get HCF.
HCF = 2² × 3 = 4 × 3 = 12

Conclusion: The HCF of 36 and 48 is 12.

 

Example 4: Find LCM of 30 and 45 using Prime Factorization

Step 1: Find the prime factorization of each number.
30 = 2 × 3 × 5
45 = 3 × 3 × 5 = 3² × 5

Step 2: Take all prime factors with the highest powers.
2¹, 3², 5¹

Step 3: Multiply these together.
LCM = 2 × 3² × 5 = 2 × 9 × 5 = 90

The LCM of 30 and 45 is 90.

 

Example 5: Prime Factorization of 60

Step 1: Divide 60 by the least prime number, which is 2.
60 ÷ 2 = 30

Step 2: Divide 30 by 2 again.
30 ÷ 2 = 15

Step 3: Divide 15 by the next prime number, 3.
15 ÷ 3 = 5

Step 4: Divide 5 by 5.
5 ÷ 5 = 1

As we have reached 1, we stop.

So, the prime factorization of 60 is 2 × 2 × 3 × 5, or in exponential form: 2² × 3 × 5

 

Conclusion

Prime factorization is a powerful mathematical tool that allows us to break down complex numbers into simpler prime numbers. Whether you use the division method or the factor tree method, knowing how to find prime factorization will make it easier to solve problems involving greatest common factors, least common multiples, and simplification of expressions.

 

Frequently Asked Questions On Prime Factorization

1. What is prime factorization?

Answer: Prime factorization is the process of breaking down a number into a product of prime numbers. A prime number is a number that has only two factors: 1 and itself.
For example, the prime factorization of 30 is:
30 = 2 × 3 × 5
All these numbers (2, 3, and 5) are prime numbers. So, the product of these primes gives back the original number.

 

2. What is the prime factorization of 42?

Answer:
To find the prime factorization of 42 using the division method, divide by the smallest prime numbers step-by-step:

Divide 42 by the smallest prime number, which is 2.
42 ÷ 2 = 21

Divide 21 by the next smallest prime number, which is 3.
21 ÷ 3 = 7

Divide 7 by 7 (since 7 is a prime number).
7 ÷ 7 = 1

As we have reached 1, we stop.

So, the prime factorization of 42 is 2 × 3 × 7.

 

3. What is a prime factor of 20?

Answer:
The number 20 can be broken into prime factors:

20 = 2 × 2 × 5
So, the prime factors of 20 are:
2 and 5

Both are prime numbers that divide 20 exactly.

 

4. What is the prime factorization of 144?

Answer:
Let’s find the prime factorization of 144 using the division method:

144 ÷ 2 = 72
72 ÷ 2 = 36
36 ÷ 2 = 18
18 ÷ 2 = 9
9 ÷ 3 = 3
3 ÷ 3 = 1

So, the prime factors are: 2 × 2 × 2 × 2 × 3 × 3
Which gives us:
144 = 2⁴ × 3²

 

5. What is 96 in prime factor form?

Answer:
To express 96 in prime factor form:

96 ÷ 2 = 48
48 ÷ 2 = 24
24 ÷ 2 = 12
12 ÷ 2 = 6
6 ÷ 2 = 3
3 ÷ 3 = 1

So, the prime factorization is: 2 × 2 × 2 × 2 × 2 × 3
In exponential form:
96 = 2⁵ × 3

 

Practice prime factorization with solved examples at Orchids The International School to make math fun and easy!