NCERT Solutions For Class 3 Maths Chapter 10 - Play with Patterns
Play with Patterns deals with patterns in geometrical shapes, patterns in even and odd numbers. This chapter have exercises on symmetrical shapes and patterns, patterns and designs with straight lines and geometrical shapes, patterns in even and odd numbers The solutions for Math-Magic Chapter-10 have been created and verified by our experienced subject matter experts, according to the CBSE syllabus and guidelines of NCERT. For practice, our subject matter experts have created very interactive, activity-based, and Image-based worksheets on these topics to enhance learning..
Download PDF For NCERT Solutions for Maths Play with Patterns
The NCERT Solutions For Class 3 Maths Chapter 10 - Play with Patterns are tailored to help the students master the concepts that are key to success in their classrooms. The solutions given in the PDF are developed by experts and correlate with the CBSE syllabus of 2023-2024. These solutions provide thorough explanations with a step-by-step approach to solving problems. Students can easily get a hold of the subject and learn the basics with a deeper understanding. Additionally, they can practice better, be confident, and perform well in their examinations with the support of this PDF.
Download PDF
Access Answers to NCERT Solutions For Class 3 Maths Chapter 10 - Play with Patterns
Students can access the NCERT Solutions For Class 3 Maths Chapter 10 - Play with Patterns. Curated by experts according to the CBSE syllabus for 2023–2024, these step-by-step solutions make Maths much easier to understand and learn for the students. These solutions can be used in practice by students to attain skills in solving problems, reinforce important learning objectives, and be well-prepared for tests.
Patterns Around Us
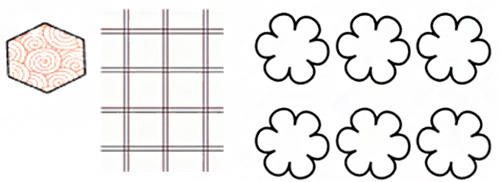
some patterns which you have found around yourself
Do it by yourself. A sample answer is:
Can you see a pattern in the way each block is repeated?
Observe the blocks in the given image. Blocks are placed upwards and downwards in a pattern. So, there is a pattern.
Look around you and list three things in which you find some pattern.
Do it by yourself. Answers may vary. You can find patterns in tiling, designs in sarees, grills, etc..
Practice Time
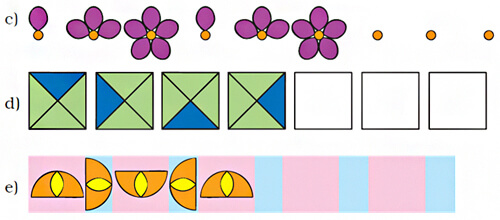
Given below are some patterns. Figure out the rule for each and continue the pattern.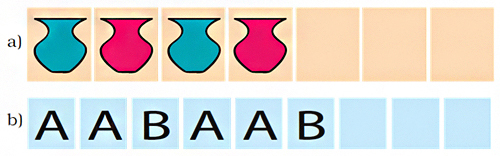
f. Morning, afternoon, evening, night, morning, ........
a. In this pattern, a blue pot and a pink pot are repeated alternatively.
b. In this pattern, one ‘B’ appears after every two ‘A’
c. In this pattern, the number of petals of the flower increases from 1 to 3 and then to 5. After that, the pattern repeats itself.
d. In this pattern, the blue colour triangle is rotating in an anticlockwise direction.
e. In this pattern, the half-circle is rotating in a clockwise direction.
f. In this pattern, the different times of a day are repeated in a manner as they arrive one by one in a day. Morning, afternoon, evening, night, morning, afternoon, evening, night.
Growing Patterns
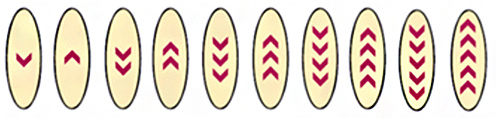
Can you see the rule and continue the pattern?
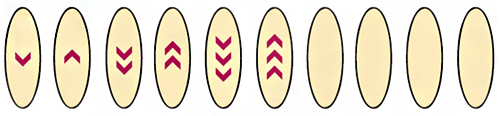
Observe the given pattern, the arrowheads are given in the opposite direction from the previous one and the number of arrowheads are increasing after every two ovals.
Try these also.
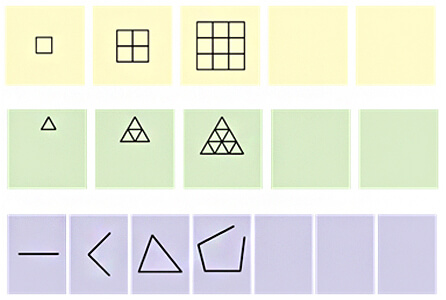
The complete patterns are shown below.
My Own Patterns
Here is your space to make your own patterns:
Do it by yourself. Answers may vary. Some sample patterns are drawn below.
1
2
3
4
Number Patterns
A. Look for the rules and continue these growing patterns: a. 51, 56, 61, 66, ____, ____, .......... b. 7, ____, 21, 28, 35, ____, ____, .......... c. 2, 4, 8, 16, 32, ____, ____, ____ d. 12A,13B,14C, ____, ____
a. Observe the given pattern, the difference between each pair of numbers is:
56 – 51 = 5, 61 – 56 = 5, 66 – 61 = 5
The numbers are increasing as well.
Therefore, the next numbers in the given patterns are:
66 + 5 = 71, 71 + 5 = 76
Hence, the pattern is:
51, 56, 61, 66, 71, 76, 81, 86 …
b.Observe the given pattern, the difference between each pair of numbers is:
28 – 21 = 7, 35 – 28 = 7
The numbers are increasing as well.
Therefore, the missing numbers are:
7 +7 = 14, 35 + 7 = 42, 42 + 7 = 49
Hence, the complete pattern is:
7, 14, 21, 28, 35, 42, 49, 56, …
c. Observe the given pattern, each number is double of the previous number.
4 = 2 × 2, 8 = 2 × 4, 16 = 2 × 8
Therefore, the missing numbers are:
2 × 32 = 64, 2 × 64 = 128, 2 × 128 = 256
Hence, the complete pattern is:
2, 4, 8, 16, 32, 64, 128, 256, …
d. Observe the given pattern, the difference between each pair of numbers is:
13 – 12 = 1,14 – 13 = 1
Also, there are capital letters of the English alphabet as a suffix with each number in the pattern A, B, C….
Therefore, the missing entries are:
(14 + 1) D = 15D, (15 + 1) E = 16E
Hence, the pattern is:
12A, 13B, 14C, 15D, 16E, 17F…
B. Look at these growing patterns. Find out what to add to each number to get the next one: a. 1, 3, 6, 10, ___, ___, ___, ___, ___.
b. 0, 2, 6, 12, ___, ___, ___, ___, ___.
c. 1, 3, 7, 13, ___, ___, ___, ___, ___.
d. 2, 3, 6, 11, 18, ___, ___, ___, ___, ___
a. Observe the difference between each pair of numbers in the given pattern.
3 – 1 = 2, 6 – 3 =3, 10 – 6 = 4
The difference is increasing in the pattern:
2, 3, 4, …
Therefore, the next numbers in thee given pattern are:
10 + 5 = 15, 15 + 6 = 21, 21 + 7 = 28, 28 + 8 = 36, 36 + 9 = 45.
Hence, the complete pattern is:
1, 3, 6, 10, 15, 21, 28, 36, 45.
b. Observe the difference between each pair of numbers in the given pattern.
2 – 0 = 2, 6 – 2 = 4, 12 – 6 = 6
The difference is increasing in the pattern:
2, 4, 6, …
Therefore, the next numbers in the given patterns are:
12 + 8 = 20, 20 + 10 = 30, 30 + 12 = 42, 42 + 14 = 56, 56 + 16 = 72.
Hence, the complete pattern is:
0, 2, 6, 12, 20, 30, 42, 56, 72
c. Observe the difference between each pair of numbers in the given pattern.
3 – 1 = 2, 7 – 3 = 4, 13 – 7 = 6
The difference is increasing in the pattern:
2, 4, 6, …
Therefore, the next numbers in the given pattern are:
13 + 8 = 21, 21 + 10 = 31, 31 + 12 = 43, 43 + 14 = 57, 57 + 16 = 73.
Hence, the complete pattern is:
1, 3, 7, 13, 21, 31, 43, 57, 73.
d. Observe the difference between each pair of numbers in the given pattern.
3 – 2 = 1, 6 – 3 = 3, 11 – 6 = 5, 18 – 11 = 7
The differences are increasing odd numbers in the pattern:
1, 3, 5, 7, …
Therefore, the next numbers in the given pattern are:
18 + 9 = 27, 27 + 11 = 38, 38 + 13 = 51, 51 + 15 = 66, 66 + 17 = 83.
Hence, the complete pattern is:
2, 3, 6, 11, 18, 27, 38, 51, 66, 83.
Secret Messages
Now you also make your own secret messages.
Do it by yourself. Answers may vary.
Can you tell what they are trying to say?
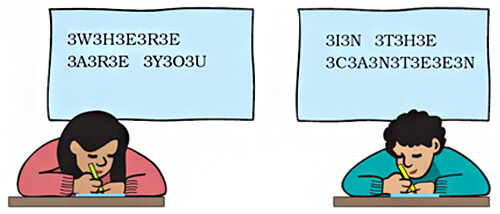
Observe the secret messages. After each 3 there is an English alphabet in the messages. Remove all 3s to decode the message.
Secret message:
‘3W3H3E3R3E
3A3R3E 3Y3O3U’
After removing 3s, the decoded message is:
‘WHERE ARE YOU’
Secret message:
‘3I3N 3T3H3E
3C3A3N3T3E3E3N’
After removing 3s, the decoded message is:
‘IN THE CANTEEN’
These are two secret messages. Look for the patterns and find the hidden sentences.
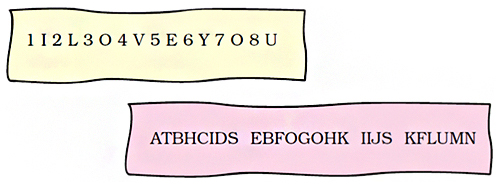
Observe the first secret message. After each number there is an English alphabet in the message. Remove all the numbers to decode the message.
Secret message:
‘1 I 2 L 3 O 4 V 5 E 6 Y 7 O 8 U’
After removing numbers, the decoded message is:
I LOVE
Observe the second secret message. Between continuous English
alphabets there are secret letters for the message. Remove the
continuous alphabets to decode the message.
Secret message:
‘ATBHCIDS EBFOGOHK IIJS KFLUMN’
Decoded message:
‘THIS BOOK IS FUN’
Even and Odd Number Patterns
What patterns do you see in these numbers? Continue the same pattern and fill in the blanks:
96, 98, ___, 102, ___, ___, ___, ___,
Observe the pattern in the given numbers. Numbers are ending with 2, 4, 6, 8, or 0. These numbers are called even numbers. The pattern is: 96, 98, 100, 102, 104, 106, 108, 110
How far can you continue this pattern?
There is no end to even numbers, this pattern can be continued without any end.
Look at the pattern of numbers in blue. Continue the pattern and fill in the blanks: 99, 101, ___,105, 107, ___, ___.
Observe the patterns in the numbers given in blue. These numbers are called odd numbers. These numbers end with 1, 3, 5, 7, or 9. The complete pattern is: 99, 101, 103, 105, 107, 109, 111, 113.
What do the numbers in the blue end with?
The numbers in the blue are odd numbers and they end with 1, 3, 5, 7, or 9.
Write all odd numbers between 400 and 410
The odd numbers between 400 and 410 are: 401, 403, 405, 407, 409
Write all even numbers between 155 and 165.
The even numbers between 155 and 165 are: 156, 158, 160, 162, 164.
If we add 1 to any odd number, we get an (even/odd) number.
If we add 1 to any even number, we get an (even/odd) number.
What do you get if you add an even number to an odd number?
If 1 is added to an even number, then the resultant number is an odd number. If 1 is added to an odd number, then the resultant number is an even number. If an even number is added to an odd number, then the resultant number is an odd number..
Names in an Order
Adil has to arrange this list so that the names starting with A come first and then come those with B, C, D, and so on. Number these names in the order in which they will come
According to the sequence of the English alphabet, the names will come in the following order..
| 1 | Aditi | 3 | Baichung |
| 3 | Elvis | 4 | Gurinder |
| 5 | Harsha | 6 | Jalaj |
| 7 | Kavitha | 8 | Mahadevan |
| 9 | Narayan | 10 | Raja |
| 11 | Sharada | 12 | Tsering |
| 13 | Warsha | 14 | 15 |
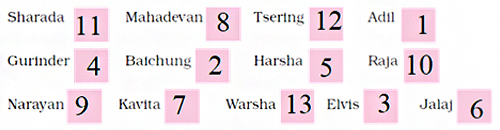
Which of the following names have the same pattern? Mark . Harsh, Anna, Kanak, Munna, Ongbi
From the given names you can observe that the names Anna Kanak can be read the same from the opposite direction as well.
Admissions Open for 2025-26
Frequently Asked Questions
The NCERT solution for Class 3 Chapter 10: Play With Patterns is important as it provides a structured approach to learning, ensuring that students develop a strong understanding of foundational concepts early in their academic journey. By mastering these basics, students can build confidence and readiness for tackling more difficult concepts in their further education.
Yes, the NCERT solution for Class 3 Chapter 10: Play With Patterns is quite useful for students in preparing for their exams. The solutions are simple, clear, and concise allowing students to understand them better. Where to Look Fromally, they can solve the practice questions and exercises that allow them to get exam-ready in no time.
You can get all the NCERT solutions for Class 3 Maths Chapter 10 from the official website of the Orchids International School. These solutions are tailored by subject matter experts and are very easy to understand.
Yes, students must practice all the questions provided in the NCERT solution for Class 3 Maths Chapter 10: Play With Patterns as it will help them gain a comprehensive understanding of the concept, identify their weak areas, and strengthen their preparation.
Students can utilize the NCERT solution for Class 3 Maths Chapter 10 effectively by practicing the solutions regularly. Solve the exercises and practice questions given in the solution.