The total length of wire is 70 metres.
The length of Rahmat’s boundary is 54 metres.
Subtract 54 m from 70 m to get the length of the extra wire.
70 – 54 = 16 m
Therefore, he gave 16 metres of wire to Ganpat
NCERT Solutions For Class 4 Maths Chapter 13 - Fields And Fences
Fields and Fences deals with the concept of area and perimeter. This chapter have exercises on finding area and perimeter of simple geometrical shapes without using formulas. The solutions for Math-Magic Chapter-13 have been created and verified by our experienced subject matter experts, according to the CBSE syllabus and guidelines of NCERT. For practice, our subject matter experts have created very interactive, activity-based, and Image-based worksheets on these topics to enhance learning.
Download PDF For NCERT Solutions for Maths Fields And Fences
The NCERT Solutions For Class 4 Maths Chapter 13 - Fields And Fences are tailored to help the students master the concepts that are key to success in their classrooms. The solutions given in the PDF are developed by experts and correlate with the CBSE syllabus of 2025-2026. These solutions provide thorough explanations with a step-by-step approach to solving problems. Students can easily get a hold of the subject and learn the basics with a deeper understanding. Additionally, they can practice better, be confident, and perform well in their examinations with the support of this PDF.
Download PDF
Access Answers to NCERT Solutions For Class 4 Maths Chapter 13 - Fields And Fences
Students can access the NCERT Solutions For Class 4 Maths Chapter 13 - Fields And Fences. Curated by experts according to the CBSE syllabus for 2025–2026, these step-by-step solutions make Maths much easier to understand and learn for the students. These solutions can be used in practice by students to attain skills in solving problems, reinforce important learning objectives, and be well-prepared for tests.
Field and Fences
Rahmat bought a roll of 70 m wire for the fence
Ganpat: Can you give me the wire that is left with you? I will use it for my field.
How much wire did Rahmat give to Ganpat?
How much more wire will Ganpat need for his field?
Length of the boundary is 66 metres. Length of the wire is 16 metres.
Subtract 16 from 66 to get the length of the wire required.
66 – 16 = 50
Therefore, Ganpat will need 50 metres more wire.
How long is the boundary of Ganpat's field?
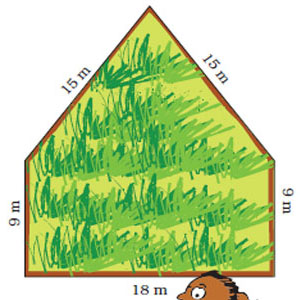
The length of the boundary is equal to the sum of the length of each side.
Add 15 m, 15 m, 9 m, 18 m, and 9 m to get the total length of the boundary.
15 m + 15 m + 9 m + 18 m + 9 m = 66 m
Therefore, the total length of the boundary is 66 metres
Rahmat needs to find the length of the boundary of the field. Can you find it from this picture? See the length of each side written near it.
_20250423_143639.jpeg)
The length of the boundary is equal to the sum of the length of each side.
Add 9 metre, 15 metre, 21 metre, and 9 metre to get the total length of the boundary.
9 m + 15 m + 21 m + 9 m = 54 m
Therefore, the total length of the boundary is 54 metres.
Practice Time
2. Chandu's father is called the young old man in his village. At 70 years of age, he is fully fit. Do you know his secret? He goes for a walk around the field every morning. Everyday he takes four rounds of Chandu's field. What is the total distance he covers? 4 × ______ = ______m = ______km.
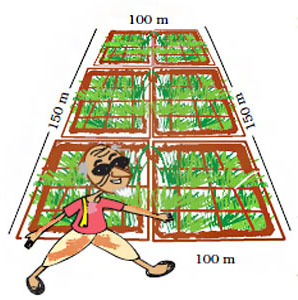
Step 1: Add 150 metres, 100 metres, 150 metres, and 100 metres to get the boundary of the field.
150 m + 100 m + 150 m + 100 m = 500 m
Step 2: He walks 4 times around the field. Multiply 500 by 4 to get the total distance he walks.
500 m × 4 = 2000 m
Step 3: Since 1000 m = 1 km, divide 2000 by 1000 to convert 2000 m to kilometres.
2000 ÷ 1000 = 2
Thus, 2000 m = 2 km.
Hence, 4 × 500 = 2000 m = 2 km.
3. Ganpat's wife works in a tailor's shop. She has to fix lace around a tablecloth. She bought a 100 metre roll of lace. Look at the picture of the table cloth and write down how much lace is used for one tablecloth.
_20250507_115858.jpeg)
Add 1 m 50 cm, 50 cm, 50 cm, and 1 m 50 cm to get the total lace that is used for one tablecloth.
1 m 50 cm + 50 cm + 50 cm + 1 m 50 cm = 2 m 200 cm.
The total lace used is 2 m 200 cm.
Since 100 cm = 1 m, 200 cm = 2m.
Hence, the total lace used is 2 + 2 = 4 metres.
How much lace will be used in 3 such tablecloths?
Length of lace used in 1 tablecloth is 4 metres.
Multiply 4 by 3 to get the length of the lace required to make three tablecloths.
4 × 3 = 12
Therefore, 12 metres of lace will be used in 3 such tablecloths.
How much lace will be left in the roll?
Total length of the lace in the roll is 100 metres. Length of lace used in 3 tablecloths is 12 metres.
Subtract 12 from 100 to get the lace that will be left in the roll.
100 m – 12 m = 88 m
Therefore, 88 metres of lace is left
Find out the length of the boundary of these shapes. (Hint: you can use a thread).
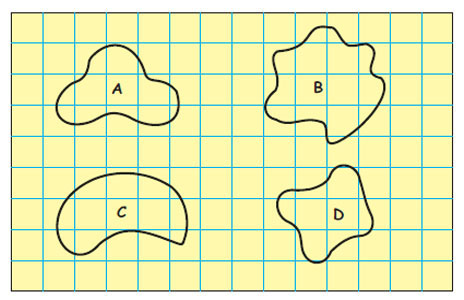
You can measure the lengths by following these steps.
a. Take a thread.
b. Move the tread over the given shapes.
c. Cut the tread which covers the boundary.
d. Measure the length of the tread.
The length of the tread will be equal to the length of the boundary. Repeat the same process for each of the shapes separately to get the length of the boundary of each shape.
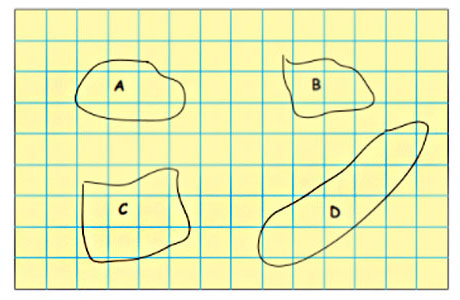
Now count the squares to find out:
How many squares are there in each shape?
It is observed from the given picture that the:
• Shape A has 1 complete square.
• Shape B has 2 complete squares.
• Shape C has 3 complete squares.
• Shape D has 2 complete squares.
Which shape covers the least number of squares?
The shape A covers the least number of squares. It covers only 1 complete square.
Which shape covers the most number of squares?
The shape C covers the most number of squares. It covers 3 complete squares.
Find out:
How many squares are there in each shape?
The answer will vary based on the shapes you have drawn in the previous answer.
The sample answer is:
The shape A has 1 complete square.
The shape B has 2 complete squares.
The shape C has 3 complete squares.
The shape D has 4 complete squares.
Which is the biggest shape?
The answer will vary based on the previous answer. The shape D is the biggest shape as it has 4 complete squares.
Which is the smallest shape?
The answers will vary.
The shape A is the smallest shape as it has 1 complete square.
How long is the boundary of each shape?
You can measure the boundary by following steps.
a. Take a thread.
b. Move the thread over the given shapes.
c. Cut the thread which covers the boundary.
d. Measure the length of the thread.
The length of the thread will be equal to the length of the boundary. Repeat the same process for each shape separately to get the length of the boundary of each shape.
3. How many different shapes can you make by joining two squares? Draw them on the squared sheet given below. How long is the boundary of each shape?
Do it by yourself as directed
- Here are pictures of some more fields. Find out which one has the longest boundary.
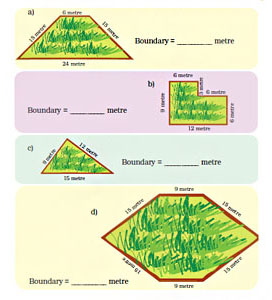
Step 1: Add 15 metres, 6 metres, 15 metres, and 24 metres to get the length of the boundary of the field a).
15 m + 6 m + 15 m + 24 m = 60 m
Therefore, the length of the boundary of the field a) is 60 metres. Step 2: Add 9 metres, 6 metres, 3 metres, 6 metres, 6 metres, and 12 metres to get the length of the boundary of the field b).
9 m + 6 m + 3 m + 6 m + 6 m + 12 m = 42 m
Therefore, the length of the boundary of the field b) is 42 metres. Step 3: Add 9 metres, 12 metres, and 15 metres to get the boundary of the field c).
9 m + 12 m + 15 m = 36 m
Therefore, the length of the boundary of the field c) is 36 metres. Step 4: Add 15 metres, 9 metres, 15 metres, 15 metres, 9 metres, and 15 metres to get the boundary of the field d).
15 m + 9 m + 15 m + 15 m + 9 m + 15 m = 78 m
Therefore, the length of the boundary of the field d) is 78 metres. Hence, field d) has the longest boundary.
Take a 20-centimetre-long thread. Make different shapes by joining the ends. Place on the squared sheet on the next page.
Make shapes of your choice. Answers may vary. One example is:
Practice Time
7. Look at the picture. Can you divide it into 4 equal pieces? Each piece should have the same number of squares.

There are 12 squares in all. It can be divided into 4 equal parts with 12 ÷ 4 = 3 squares in each part.
b) If you cut a 1 cm square to get shape C, what will be the length of the boundary of C?
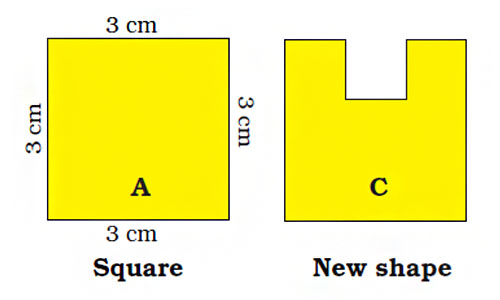
The correct answer is:A square of 1 cm is cut off. The length of the remaining sides of the square C is shown in the following diagram
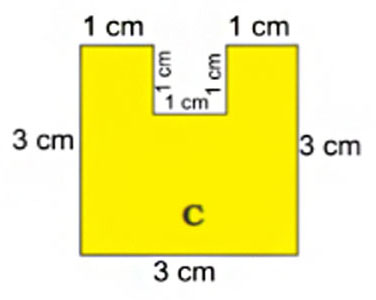
The length of the boundary is equal to the sum of the length of each side. Add 3 cm, 3 cm, 3 cm, 1 cm, 1 cm, 1 cm, 1 cm, and 1 cm.
3 cm + 3 cm + 3 cm + 1 cm + 1 cm + 1 cm + 1 cm + 1 cm = 14 cm.
Therefore, the length of the boundary of square C is 14 cm.
5. a) How many small squares of size 1 cm are there in this big green square?

By counting each square, it is observed that there are 36 squares of size 1 cm in all.
5. Guess how many squares of one centimetre can fill this blue rectangle.
Write your guess here. _________
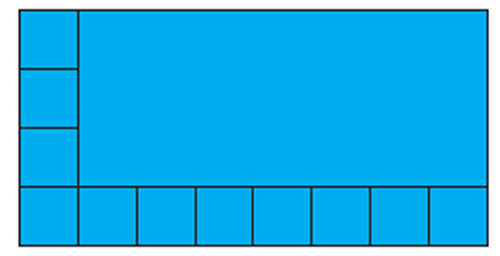
Answers may vary from student to student. Observe the number of squares on the bottom line and guess the number of squares required to fill the blue rectangle.
The correct answer is 21
c) 8 squares of side 1 cm are cut out of the square D. Now it looks like shape E. What is the length of the boundary of shape E?

It is observed from the given figure that there are 36 sides and each side is 1 cm in length. The length of the boundary is equal to the sum of the length of each side.
The boundary length of the figure E is equal to 1 cm added 36 times, that is 36 cm. Hence, the length of the boundary of shape E is 36 cm.
c) The boundary of this is 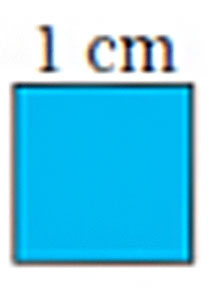 ____ + ____ + ____ + ____. Can we also say that the boundary is 4 × 1 cm?
____ + ____ + ____ + ____. Can we also say that the boundary is 4 × 1 cm?
The boundary of the given square is 1 cm + 1 cm + 1 cm + 1 cm = 4cm. A square has 4 sides. Length of each side of the square is 1 cm. Therefore, we can also say that the boundary length is 4 × 1 cm = 4 cm.
Raghavan has a piece of land. There are 4 houses on his land and in the middle there is a well. He wants to divide this land equally among his four children. Each should get one house and should be able to use the well without entering the other's land. Can you help him divide the land?
Give different colours to each one's share.
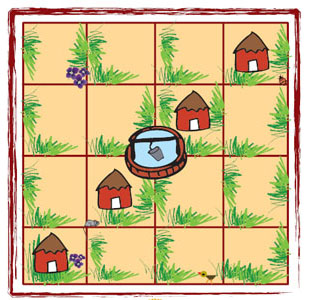
The land is divided into 12 small squares. Each child should get one house in a way that they should be able to use the well without entering the other's land.
The answer may vary. One sample answer is:

The above picture shows the division of the land equally among four children. The land of each child has four small squares with one house each.
2. a) Find the length of the boundary of square D.
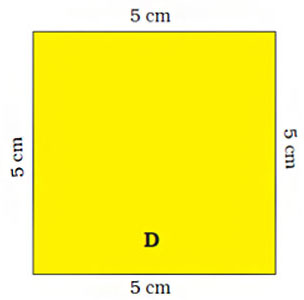
The length of the boundary is equal to the sum of the length of each side. Add 5 cm four times to get the length of the boundary of D.
5 cm + 5 cm + 5 cm + 5 cm = 20 cm.
Therefore, the length of the boundary of square D is 20 cm.
Check your guess by filling it with small squares.
Draw a square of size 1 cm on the blue rectangle. The complete drawing is shown below:
It is observed that there are 32 squares in total. Therefore, 21 more squares were made to complete the rectangle.

3. A hockey field is 91 metres 40 cm long and 55 metres wide. How long is the boundary of the field?
The field is rectangular in shape. It has four sides. Opposite sides are equal in shape. The drawing of the hockey field is shown below.
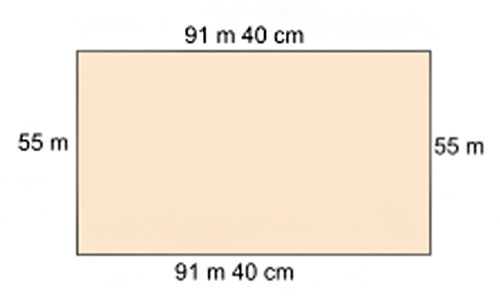
The length of the boundary of the field is the sum of the length of each side.
Add 55 m, 91 m 40 cm, 55 m and 91 m 40 cm to get the boundary length.
55 m + 91 m 40 cm + 55 m + 91 m 40 cm = 292 m 80 cm
Therefore, the boundary length of the hockey field is 292 m 80 cm
4. a) Which is the biggest leaf in this picture?

The leaf in the middle from the top is the biggest.
The biggest leaf is shaded in the picture below:

- A square has a boundary of 12 cm.
a) From the corner of this square, a small square of 1 cm is cut off. Will the boundary of B be less or more? Find its length
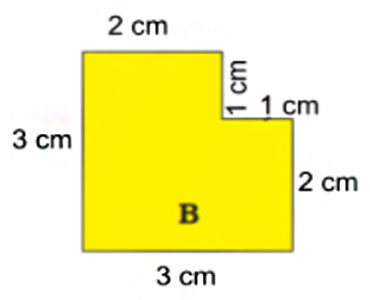
A square of 1 cm is cut off from the side. The length of the remaining sides of square B is shown in the following diagram

The length of the boundary is equal to the sum of the length of each side. Add 3 cm, 3 cm, 2 cm, 1 cm, 1 cm, and 2 cm.
3 cm + 3 cm + 2 cm + 1 cm + 1 cm + 2 cm = 12 cm.
Therefore, the length of the boundary of square B is same as that of square A and it is equal to 12 cm.
Have you seen any race where runners start from different places — like in this picture? Guess why?
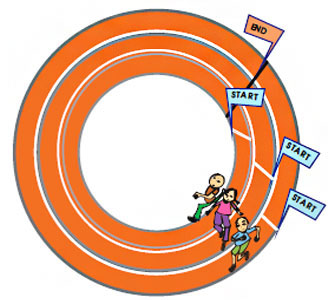
Answer this question based on your experience. Answers may vary. In a circular track race, the runner starts from different places so as to cover the equal distance.
How will Neetu find out if the two gardens are equally big?
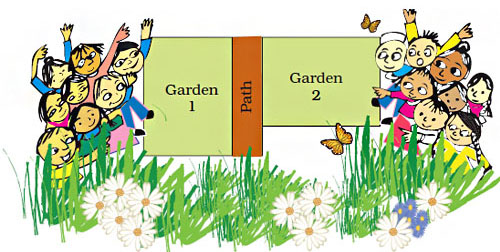
Answers may vary from student to student. One example is: Use a thread and trace the outer boundary of each garden separately. Then measure the length of each. If the length of the threads are equal then the two gardens are equal.
Activity
1. Look at the table in your classroom. Guess how many MathMagic books you can place on it. (Remember — The books should not overlap. Do not leave gaps between the books) Write your guess here.
Answers will vary according to the size of the table. Observe the size of the table in your classroom and the size of the book to answer the question.
Now check if your guess was right. How many books could you place?
Answers may vary based on the size of the table and the guess made in the previous answer. Put the books on the table of your classroom in a way that there is no gap between any two books and also in none of the books overlap.
Count the number of books that are placed on the table. Check if it is the same as the number you guessed.
What is the difference between your guess and the actual number of books?
Answers may vary. Note down the guessed number and the actual number and then subtract the larger number from the smaller number to get the difference between your guess and the actual number of books.
2. Now look for another table.
a) Is this table bigger than the last table? Yes/No
Answers may be different based on the selection of the new table. Observe the size of both the tables and answer.
b) Make a guess how many Math-Magic books can be kept on this table.
Answers will vary according to the size of the new table. Observe the size of the new table and the size of the book to answer the question.
c) Check if your guess was correct. How many Math-Magic books could you keep?
Answers may vary based on the size of the new table and the guess made in the previous answer. Put the books on the new table in such a way that there is no gap between any two books and also in a way that none of the books overlap.
Count the number of books that are placed on the table. Check if it is the same as the number you guessed.
d) The difference between the sizes of the two tables is __________ books.
Answers may vary. Write the difference between the number of books placed on the two tables.
3. a) How many Math-Magic books can be covered with one sheet of newspaper?
With one sheet of newspaper, 4 books can be covered.
b) Try covering your Math-Magic book with half a sheet of newspaper.

Perform the activity on your own.
c) Can you cover your book with a smaller sheet?
Yes, the book can be covered with a sheet smaller than that of a half sheet of a newspaper.
d) Find the smallest sheet which can cover your book. Check if your friend used a smaller sheet than you did.
Cover your book with the smallest sheet. Observe the sheet used by your friend to cover the book. Answers may vary.
b) Collect some leaves from the garden. Place each of them here on this squared sheet. Trace out their edges and check how many squares there are in each leaf
Perform the activity on your own. Answers may vary based on the leaves collected from the garden
d) Which is the smallest leaf?
The answer will vary based on the leaves collected and traced. Observe the size of the leaves on the sheets and check which is the smallest leaf.
b) Can you think of a faster way to know the total number of small squares without counting each?
There are 6 squares in 1 row and there are 6 such rows. Therefore, the total number of squares can be counted as
6 × 6 = 36
c) Which is the biggest leaf?
The answer will vary based on the leaves collected and traced. Observe the size of the leaves on the sheets and check which is the biggest leaf.
4. Usha and Valsamma are running a race. Usha is running on the inner circle. Valsamma is running on the outer circle. Valsamma runs faster than Usha. But still she loses the race. Can you guess why?

Usha was running on the outer circle whereas Valsamma was running on the outer circle. So, the distance that Usha had to run was less than the distance that Valsamma had to run. Therefore, though the speed of Valsamma was more she lost the race as her distance was more.
Admissions Open for
Admissions Open for
Frequently Asked Questions
The NCERT solution for Class 4 Chapter 13: Fields And Fences is important as it provides a structured approach to learning, ensuring that students develop a strong understanding of foundational concepts early in their academic journey. By mastering these basics, students can build confidence and readiness for tackling more difficult concepts in their further education.
Yes, the NCERT solution for Class 4 Chapter 13: Fields And Fences is quite useful for students in preparing for their exams. The solutions are simple, clear, and concise allowing students to understand them better. They can solve the practice questions and exercises that allow them to get exam ready in no time.
You can get all the NCERT solutions for Class 4 Maths Chapter 13 from the official website of the Orchids International School. These solutions are tailored by subject matter experts and are very easy to understand.
Yes, students must practice all the questions provided in the NCERT solution for Class 4 Maths Chapter 13: Fields And Fences as it will help them gain a comprehensive understanding of the concept, identify their weak areas, and strengthen their preparation.
Students can utilize the NCERT solution for Class 4 Maths Chapter 13 effectively by practicing the solutions regularly. Solve the exercises and practice questions given in the solution.
CBSE Schools In Popular Cities
- CBSE Schools in Bangalore
- CBSE Schools in Mumbai
- CBSE Schools in Pune
- CBSE Schools in Hyderabad
- CBSE Schools in Chennai
- CBSE Schools in Gurgaon
- CBSE Schools in Kolkata
- CBSE Schools in Indore
- CBSE Schools in Sonipat
- CBSE Schools in Delhi
- CBSE Schools in Rohtak
- CBSE Schools in Bhopal
- CBSE Schools in Aurangabad
- CBSE Schools in Jabalpur
- CBSE Schools in Jaipur
- CBSE Schools in Jodhpur
- CBSE Schools in Nagpur
- CBSE Schools in Ahmednagar
- CBSE School In Tumkur











