a) Do it by yourself. Answers may vary.
b) Guess on your own and answer the question.
c) As shown on the ruler, the length of the pencil is 3.6 cm. Check how close your guess was.
NCERT Solutions Maths Class 5 Chapter 10 - Tenths And Hundredths
The chapter Tenths and Hundredths focuses on introducing the idea of decimals to students. It helps the students to understand the concept of the tenth or the hundredth of any given number. It covers the topics: philosophy Measuring small values in millimetres philosophy Relative measurement units philosophyDifferences in sizes philosophyEstimating values NCERT Math-Magic questions are answered in a simple and engaging manner. We have also related 'Learning Concepts and interactive worksheets with the solutions. Our 'Learning Beyond' segment caters to all the probable questions that a child might think out of curiosity. Download Chapter 10 Tenths and Hundredths in PDF format for free here.
Download PDF For NCERT Solutions for Maths Tenths And Hundredths
The NCERT Solutions Maths Class 5 Chapter 10 - Tenths And Hundredths are tailored to help the students master the concepts that are key to success in their classrooms. The solutions given in the PDF are developed by experts and correlate with the CBSE syllabus of 2025-2026. These solutions provide thorough explanations with a step-by-step approach to solving problems. Students can easily get a hold of the subject and learn the basics with a deeper understanding. Additionally, they can practice better, be confident, and perform well in their examinations with the support of this PDF.
Download PDF
Access Answers to NCERT Solutions Maths Class 5 Chapter 10 - Tenths And Hundredths
Students can access the NCERT Solutions Maths Class 5 Chapter 10 - Tenths And Hundredths. Curated by experts according to the CBSE syllabus for 2025–2026, these step-by-step solutions make Maths much easier to understand and learn for the students. These solutions can be used in practice by students to attain skills in solving problems, reinforce important learning objectives, and be well-prepared for tests.
Tenths and Hundredths
a) What was the length of the smallest pencil you have used?
b) How long is this pencil? Guess___ cm 
c) Measure it using a scale. How good is your guess?
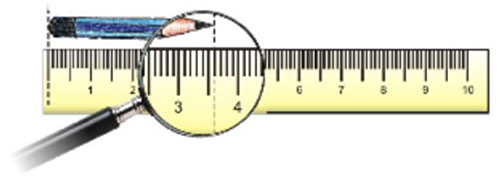
a) What is the length of this pencil? __mm.
b) What is the length of this pencil in centimetres?
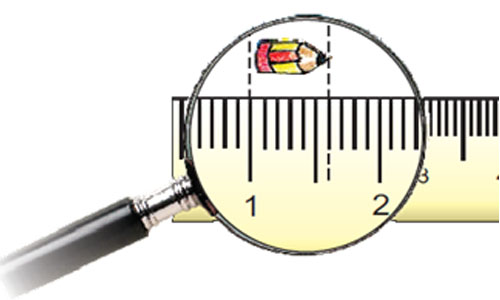
a) The length of the pencil is 6 mm.
b) The length of the pencil is 0.6 cm.
Frogs
a) What does 0.9 cm mean? It is the same as __ millimetres.
b) We can also say this is nine-tenths of a cm. Right?
c) So, 30.5 cm is the same as __ cm and __ millimetre.
d) About how many of the big frogs will fit on the 1 m scale? ___
e) If they sit in a straight line about how many of the small frogs will cover 1 m? ___
a) The relation between cm and mm is: 0.1 cm = 1 mm
b) 1 mm is one-tenth of a cm. So, we can say 9 mm is nine-tenth of a cm.
c) 30.5 cm is the same as 30 cm and 5 mm.
d) The relation between m and cm is: 1 m = 100 cm Since 1 big frog is 30.5 cm long, about 3 big frogs will fit on the 1 m scale.
e) Since 1 small frog is 0.9 cm long, about 111 small frogs will cover 1 m.
Practice Time
How many paise does a matchbox cost?
The cost of a matchbox is Rs 0.50.
1 rupee = 100 paise
⇒ 0.50 rupee = 50 paise.
Therefore, the cost of a match box is 50 paise.
How many matchboxes can be got for Rs 2.50?
Rs 0.50 is the cost of 1 matchbox.
Therefore, Rs 2.50 is the cost of 2.50 ÷ 0.50 = 5 matchboxes.
Thus, 5 matchboxes can be bought for Rs 2.50.
How many rupees does the soap cost?
The soap cost Rs 8.75.
Arun wanted to buy a soap. He has a five-rupee coin, 2 one-rupee coins and 4 half-rupee coins. Write in rupees what money he will get back.
Arun has:
1 five-rupee coin = Rs 5
2 one-rupee coins = Rs 2
4 half-rupee coins = Rs 2
Total amount = 5 + 2 + 2 = Rs 9
Since the cost of a soap is Rs 8.75, he will get back
9 – 8.75 = Rs 0.25.
a) An egg costs two and a half rupees. How much will one and a half dozen cost?
b) How many pens can Kannan buy? How much money is left?

a) Since one dozen eggs = 12 eggs, we have
one and half dozen eggs = 12 + 6 = 18 eggs.
The cost of 1 egg = Rs 2.50
⇒ the cost of 18 eggs = 18 × 2.50 = 45
Therefore, one and half dozen eggs will cost Rs 45.
b) He spent Rs 45 in buying eggs. The amount left is:
60 – 45 = Rs 15.
Since one pen costs Rs 6.50, he can buy 2 pens for Rs 15.
What is Dinesh’s height in metres? __ m __ cm.

We know that 1 m = 100 cm. Therefore,
2 m = 200 cm
Since he need to grow 45 cm more to reach 2 m height, his present height is
200 – 45 = 155 cm.
Now, convert 155 cm in m and cm as:
155 cm = 1.55 m = 1 m 55 cm
Therefore, Dinesh’s height is 1.55 m or 1 m 55 cm.
Length of the nail — 2 cm and __ mm or 2. __ cm.
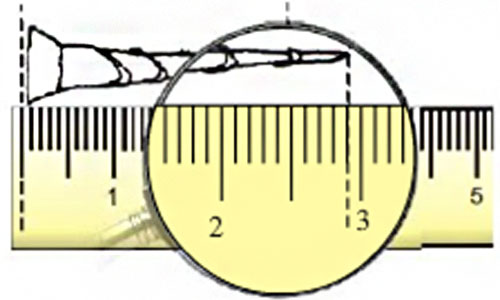
The length of the nail is 2 cm and 9 mm. Since 1 mm = 0.1 cm, we can write 2 cm and 9 mm also as 2.9 cm.
The price of two pens is Rs __.
Can she buy two pens?

The price of one pen is Rs 6.50
⇒ The price of two pens = 2 × 6.50 = Rs 13
Therefore, she can buy two pens for Rs 13.
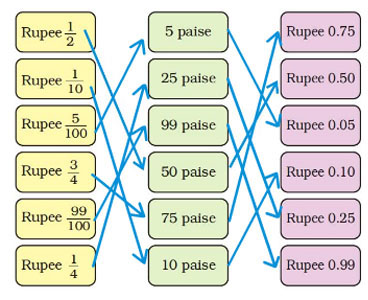
Match each yellow box with one green and one pink box.
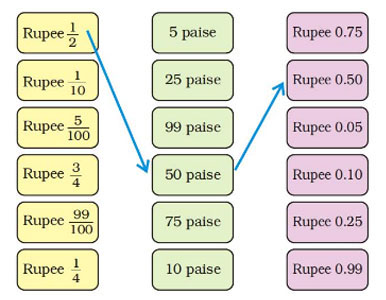
Match the rupee with equivalent paise, and the rupee written in decimals. The correct answer is:
a) What part of this sheet is coloured blue?__/10
b) What part of the sheet is green? __
c) Which colour covers 0.2 of the sheet?
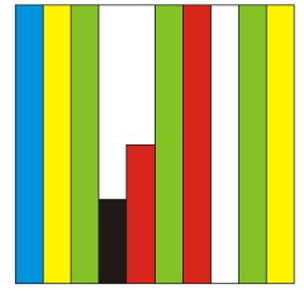
The sheet can be divided into 10 long strips. So, each long strip is 1/10 or 0.1 of the sheet.
a) 1 strip is coloured blue. Therefore,
part of the sheet is coloured blue.
b) Three strips are coloured green. Therefore,
or 0.3 part of the sheet is green.
c) There are 2 yellow strips. Therefore, the yellow colour covers or 0.2 of the sheet.
a) Look at the second sheet. Each strip is divided into 10 equal boxes. How many boxes are there in all?
b) Is each box 1/100 part of the sheet? How many blue boxes are there? __ Is blue equal to 10/100 of the sheet? We saw that blue is also equal to 1/10 of the sheet. We wrote it as 0.1 of the sheet. Can we say 10/100 = 1/10 = 0.10 = 0.1?
c) Can we write ten paise as 0.1 of a rupee?
d) How many boxes are red? What part of the sheet is this? 15/__ Can we also write it as 0.15 of the sheet?
e) Now 3/100 of the sheet is black. We can say 0.__ sheet is black.
f) How many white boxes are there in the sheet? What part of the second sheet is white? ___
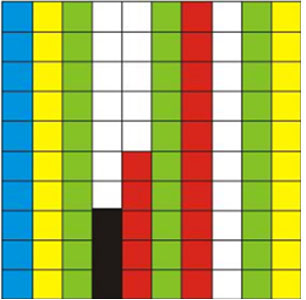
a) Observe the given sheet. Each strip is divided into 10 equal boxes, and there are 10 strips in all.
Therefore, the total number of boxes is:
10 × 10 = 100
So, there are 100 boxes in all.
b) Since there are 100 equal boxes, each box is 1/100 of the sheet.
There are 10 blue boxes. So, the blue portion is 10/100 of the sheet.
10/ 100 = 1/10 = 0.10 = 0.1
c) There are 100 paise in one rupee. Therefore,
10 paise = 10/100 rupee = 1/10 rupee = 0.10 rupee = 0.1 rupee
d) There are 15 red boxes. Since the sheet is divided into 100 equal boxes, the red colour is 15/100 of the sheet.
15/100 = 0.15
So, the red colour is 0.15 of the sheet.
e) 3/100 of the sheet is black.
3/100 = 0.30
Therefore, 0.30 of the sheet is black.
f) There are 22 white boxes. Since there are 100 boxes in all, 22/100 part of the sheet is white.
Using the scale on this page find the difference in length between candle 1 and candle 3.
| Length of | Length in cm and mm | Length in cm |
|---|---|---|
| Candle 1 | ||
| Flame 1 | ||
| Candle 2 | ||
| Flame 2 | ||
| Candle 3 | ||
| Flame 3 |

Using a ruler measure the length of the candles and their flames and write your findings in the given table as shown below.
| Length of | Length in cm and mm | Length in cm |
|---|---|---|
| Candle 1 | 2 cm 9 mm | 2.9 cm |
| Flame 1 | 1 cm 3 mm | 1.3 cm |
| Candle 2 | 4 cm 9 mm | 4.9 cm |
| Flame 2 | 1 cm 9 mm | 1.9 cm |
| Candle 3 | 6 cm | 6 cm |
| Flame 3 | 1 cm 9 mm | 1.9 cm |
Since the length of candle 1 is 2.9 cm and candle 3 is 6 cm, the difference in length is: 6 – 2.9 = 3.1 cm
What is the length of a 100 rupee note? Guess. Now measure it using a scale. Now guess the length and width of many other things. Measure and find the difference between your measure and your guess.
| size of | Your guess in cm | Your measure in cm | ||
|---|---|---|---|---|
| length | width | length | width | |
| 100 Rupee note | ||||
| 10 Rupee note | ||||
| 20 Rupee note | ||||
| 5 Rupee note | ||||
| Post card | ||||
| Math-Magic book | ||||
Do it by yourself. Answers may vary. A sample answer is:
| size of | Your guess in cm | Your measure in cm | ||
|---|---|---|---|---|
| length | width | length | width | |
| 100 Rupee note | 17 | 9 | 15.7 | 7.2 |
| 10 Rupee note | 12 | 8 | 13.6 | 6.4 |
| 20 Rupee note | 11 | 7 | 14.6 | 6.3 |
| 5 Rupee note | 10 | 6 | 11.8 | 6.3 |
| Post card | 13 | 8 | 10.5 | 6.5 |
| Math-Magic book | 30 | 22 | 24 | 19.3 |
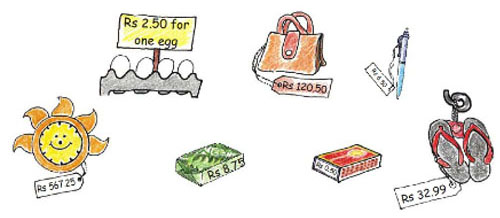
At the market
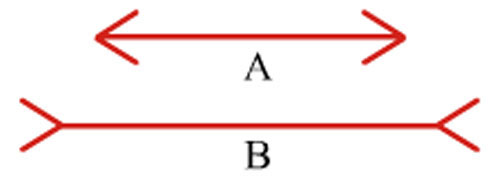
a) Which line is longer? A or B? Measure each line and write how long it is in centimetres. How good is your guess?
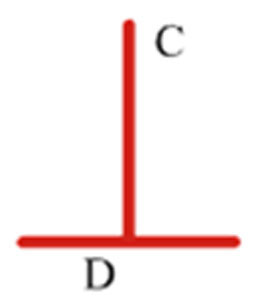
b) Which line is longer? C or D? Measure each line. How good is your guess?
a) Guess on your own. Use a ruler to measure the length of the lines. The line A is 4.6 cm, and the line B is also 4.6 cm. Therefore, both the lines are equal in length.
b) Guess on your own. Use a ruler to measure the length of the given lines. The line C is 3.2 cm, and the line D is also 3.2 cm. Therefore, both the lines are the same in length.
The school at Malappuram has its sports day. The first five children in the Long Jump are:

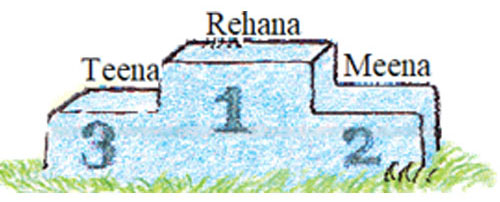
Who is the winner in the long jump? ___ Write the names of the I, II and III winners on this stand.
We can also write 1 cm as __m.
Observe the given table and arrange the jumps in descending order. 4.50 > 4.05 > 3.50 > 3.35 > 3.05
Therefore, Rehana is the winner, and the names of the I, II and III winners are Rehana, Meena, and Teena, respectively.
Since 100 cm = 1 m,
1 cm = 0.01 m
The length of this lady’s finger (bhindi) is __ cm and __ mm. We can also write it as __ cm.

The length of the lady’s finger is 8 cm and 4 mm. Since 1 mm = 0.1 cm, we can also write it as 8.4 cm.
Write in Metres
3 metre 45 centimetre ___ metres
99 centimetre __ metres
1 metre and 5 centimetre __ metres
Since 1 cm = 0.01 m, we have
3 metre 45 centimetre = 3.45 metres
99 centimetre = 0.99 metres
1 metre and 5 centimetre = 1.05 metres
Guess the lengths to draw these things. Ask your friend to draw the same. After you make the drawing use a scale to measure the length. Whose drawing showed a better guess?
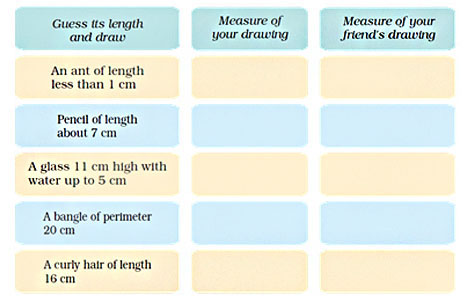
Do it by yourself. Answers may vary.
Money
Money from different countries
Shivam Bank has a chart to show us how many Indian rupees we can get when we change the money of different countries.
| Country | Money | Changed into Indian Rupees |
|---|---|---|
| Korea | Won | 0.04 |
| Sri Lanka | Rupee (SL) | 0.37 |
| Nepal | Rupee | 0.63 |
| Hong Kong | Dollar (HK) | 5.10 |
| South Africa | Rand | 5.18 |
| U.A.E. | Dirham | 10.80 |
| U.S.A. | Dollar | 39.70 |
| England | Pound | 77.76 |
| China | Yuan | 5.50 |
A) The money of which country will cost the most in Indian Rupees?
B) Mithun’s uncle in America had sent him 10 USA dollars as a gift. Mithun used 350 rupees for a school trip. How much money was left with him?
C) Majeed’s father is working in Saudi Arabia. He gets 1000 Saudi Riyal as salary. Arun’s father who is working in Sri Lanka gets 2000 Sri Lankan Rupees. Who gets more Indian rupees as salary?
D) Leena’s aunty brought a present for her from China. It cost 30 Yuan. Find what it costs in Indian rupees.
E) Astha wants some Hong Kong Dollars and Won.
1) How many Won can she change for Rs 4? For Rs 400?
2) How many Hong Kong Dollars can she change for Rs 508?
A) Observe the given chart. England's currency Pound is the most expensive.
1 Pound = Rs 77.76
B) Observe the given chart.
1 Dollar = Rs 39.70
Therefore,
10 Dollars = 10 × 39.70 = Rs 397
Since Mithun used Rs 350 for a school trip, the amount left
397 – 350 = 47
Therefore, Mithun has Rs 47 left with him.
C) From the given chart consider the exchange rate of Dirham instead of Saudi Riyal.
1 Dirham = Rs 10.80
⇒1000 Dirhams = 1000 × 10.80 = Rs10800
So, Majeed’s father’s salary is Rs 10800.
Now, consider the exchange rate of Sri Lankan rupee, Rupee (SL) from the chart.
1 Rupee (SL) = Rs 0.37
⇒ 2000 Rupee (SL) = 2000 × 0.37 = Rs 740
So, Arun’s father’s salary is Rs 740.
Hence, Majeed’s father earns more than Arun’s father.
D) Consider the exchange rate for Yuan from the given chart.
1 Yuan = Rs 5.50
⇒30 Yuan = 30 × 5.50 = Rs 165
Therefore, the present cost is Rs 165.
E) Look for the exchange rate for Won and Dollar (HK)
1) Rs 0.04 = 1 Won
⇒ Rs 1 = (1 ÷ 0.04) Won
⇒ Rs 4 = (4 ÷ 0.04) Won = 100 Won
⇒ Rs 400 = 100 × 100 Won = 10000 Won
Hence, Rs 4 = 100 Won, Rs 400 = 10000 Won
2) Rs 5.10 = 1 Dollar (HK)
⇒Rs 1 = (1 ÷ 5.10) Dollar (HK)
⇒Rs 510 = (510 ÷ 5.10) Dollar (HK) = 100 Dollar (HK)
So, for Rs 510 she can change 100 Dollar (HK)
For 99 Dollar (HK), she needs to exchange 510 – 5.10 = Rs 504.90
Since 504.9 < 508, she can change 99 Dollar (HK) for Rs 508.
Kiran went shopping with Rs 200. Look at the bill. The shopkeeper forgot to put the point correctly in the prices. Put the point in the correct place and find out the total amount of the bill.
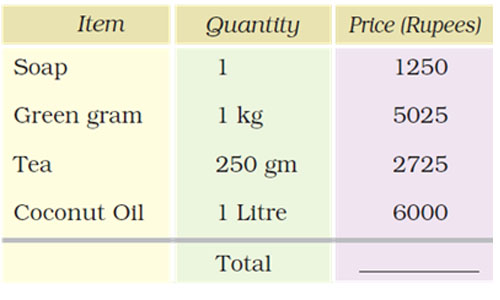
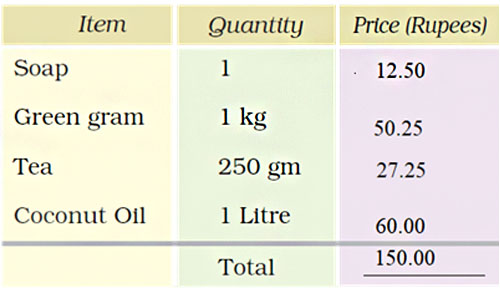
The correct answer is:
Temperature
Which city is colder?
The temperature in each city was noted at 3 pm on 16 January 2008.
1) Which place had the highest temperature at 3 pm? Which place is the coolest at that time?
2) How much higher is the temperature in Mumbai from that in Srinagar?
3) How many degrees will the temperature need to rise for it to reach 40°C in Thiruvananthapuram?
4) How much lower is the temperature in Kolkata from that in Chennai?
5) The temperature in these cities was also noted at 3 am on the same day. Look at the table and answer the questions.
a) Which place had the lowest temperature at 3 am? Imagine yourself to be there and describe how it would feel.
b) What is the difference between the temperatures at 3 pm and 3 am in Chennai? In Bhopal?
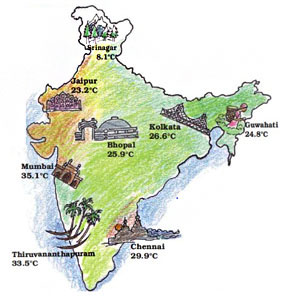
1) The temperature in Mumbai was 35.1oC, which was also the highest temperature at 3 pm. Srinagar was the coolest place at same time.
2) The difference between the temperatures of Mumbai and Srinagar was: 35.1 – 8.1 = 27
Therefore, the temperature in Mumbai is 27oC higher than Srinagar.
3) Thiruvananthapuram’s temperature should rise
40 – 33.5 = 6.5oC to reach 40oC.
4) The temperature in Kolkata is
29.9 – 26.6 = 3.3oC lower than Chennai.
5) a) At 3 a.m., Srinagar had the lowest temperature. Imagine yourself there at such a low temperature and answer the question.
b) In Chennai:
Temperature at 3 pm = 29.9oC
Temperature at 3 am = 21.1oC
> Difference 29.9 – 21.1 = 8.8oC
In Bhopal:
Temperature at 3 pm = 25.9oC
Temperature at 3 am = 9.8oC
The difference = 25.9 – 9.8 = 16.1oC
Admissions Open for
Admissions Open for
Frequently Asked Questions
The NCERT solution for Class 5 Chapter 10: Tenths And Hundredths is important as it provides a structured approach to learning, ensuring that students develop a strong understanding of foundational concepts early in their academic journey. By mastering these basics, students can build confidence and readiness for tackling more difficult concepts in their further education.
Yes, the NCERT solution for Class 5 Chapter 10: Tenths And Hundredths is quite useful for students in preparing for their exams. The solutions are simple, clear, and concise allowing students to understand them better. They can solve the practice questions and exercises that allow them to get exam-ready in no time.
You can get all the NCERT solutions for Class 5 Maths Chapter 10 from the official website of the Orchids International School. These solutions are tailored by subject matter experts and are very easy to understand.
Yes, students must practice all the questions provided in the NCERT solution for Class 5 Maths Chapter 10: Tenths And Hundredths as it will help them gain a comprehensive understanding of the concept, identify their weak areas, and strengthen their preparation.
Students can utilize the NCERT solution for Class 5 Maths Chapter 10 effectively by practicing the solutions regularly. Solve the exercises and practice questions given in the solution.
CBSE Schools In Popular Cities
- CBSE Schools in Bangalore
- CBSE Schools in Mumbai
- CBSE Schools in Pune
- CBSE Schools in Hyderabad
- CBSE Schools in Chennai
- CBSE Schools in Gurgaon
- CBSE Schools in Kolkata
- CBSE Schools in Indore
- CBSE Schools in Sonipat
- CBSE Schools in Delhi
- CBSE Schools in Rohtak
- CBSE Schools in Bhopal
- CBSE Schools in Aurangabad
- CBSE Schools in Jabalpur
- CBSE Schools in Jaipur
- CBSE Schools in Jodhpur
- CBSE Schools in Nagpur
- CBSE Schools in Ahmednagar
- CBSE School In Tumkur











