NCERT solutions for class 7 maths chapter 5 Lines and Angles

(i) Two angles are said to be complementary if the sum of their measures is 90o.

The given angle is 20o

Let the measure of its complement be xo.

Then,

= x + 20o = 90o

= x = 90o – 20o

= x = 70o

Hence, the complement of the given angle measures 70o.

(ii) Two angles are said to be complementary if the sum of their measures is 90o.

The given angle is 63o

Let the measure of its complement be xo.

Then,

= x + 63o = 90o

= x = 90o – 63o

= x = 27o

Hence, the complement of the given angle measures 27o.

(iii) Two angles are said to be complementary if the sum of their measures is 90o.

The given angle is 57o

Let the measure of its complement be xo.

Then,

= x + 57o = 90o

= x = 90o – 57o

= x = 33o

Hence, the complement of the given angle measures 33o.

 

(i) We have to find the sum of given angles to identify whether the angles are complementary or supplementary.

Then,

= 65o + 115o

= 180o

If the sum of two angle measures is 180o, then the two angles are said to be supplementary.

∴ These angles are supplementary angles.

(ii) We have to find the sum of given angles to identify whether the angles are complementary or supplementary.

Then,

= 63o + 27o

= 90o

If the sum of two angle measures is 90o, then the two angles are said to be complementary.

∴ These angles are complementary angles.

(iii) We have to find the sum of given angles to identify whether the angles are complementary or supplementary.

Then,

= 112o + 68o

= 180o

If the sum of two angle measures is 180o, then the two angles are said to be supplementary.

∴ These angles are supplementary angles.

(iv) We have to find the sum of given angles to identify whether the angles are complementary or supplementary.

Then,

= 130o + 50o

= 180o

If the sum of two angle measures is 180o, then the two angles are said to be supplementary.

∴ These angles are supplementary angles.

(v) We have to find the sum of given angles to identify whether the angles are complementary or supplementary.

Then,

= 45o + 45o

= 90o

If the sum of two angle measures is 90o, then the two angles are said to be complementary.

∴ These angles are complementary angles.

(vi) We have to find the sum of given angles to identify whether the angles are complementary or supplementary.

Then,

= 80o + 10o

= 90o

If the sum of two angle measures is 90o, then the two angles are said to be complementary.

∴ These angles are complementary angles.

 

Let the measure of the required angle be xo.

We know that the sum of measures of complementary angle pair is 90o.

Then,

= x + x = 90o

= 2x = 90o

= x = 90/2

= x = 45o

Hence, the required angle measure is 45o.

 

Let the measure of the required angle be xo.

We know that the sum of measures of supplementary angle pair is 180o.

Then,

= x + x = 180o

= 2x = 180o

= x = 180/2

= x = 90o

Hence, the required angle measure is 90o.

 

From the question, it is given that

∠1 and ∠2 are supplementary angles.

If ∠1 is decreased, then ∠2 must be increased by the same value. Hence, this angle pair remains supplementary.

 

(i) No. If two angles are acute, which means less than 90o, then they cannot be supplementary because their sum will always be less than 90o.

(ii) No. If two angles are obtuse, which means more than 90o, then they cannot be supplementary because their sum will always be more than 180o.

(iii) Yes. If two angles are right, which means both measure 90o, then they can form a supplementary pair.

∴ 90o + 90o = 180

 

Let us assume the complementary angles be p and q,

We know that the sum of measures of complementary angle pair is 90o.

Then,

= p + q = 90o

It is given in the question that p > 45o

Adding q on both sides,

= p + q > 45o + q

= 90o > 45o + q

= 90o – 45o > q

= q < 45o

Hence, its complementary angle is less than 45o.

 

(i) By observing the figure, we can say that

∠1 and ∠4, ∠5 and ∠2 + ∠3 are vertically opposite angles. Because these two angles are formed by the intersection of two straight lines.

(ii) By observing the figure, we can say that,

∠1 and ∠5, ∠5 and ∠4, as these have a common vertex and also have non-common arms opposite to each other.

 

∠1 and ∠2 are not adjacent angles because they are not lying on the same vertex.

(i) ∠x = 55o, because vertically opposite angles.

∠x + ∠y = 180o … [∵ linear pair]

= 55o + ∠y = 180o

= ∠y = 180o – 55o

= ∠y = 125o

Then, ∠y = ∠z … [∵ vertically opposite angles]

∴ ∠z = 125o

(ii) ∠z = 40o, because vertically opposite angles.

∠y + ∠z = 180o … [∵ linear pair]

= ∠y + 40o = 180o

= ∠y = 180o – 40o

= ∠y = 140o

Then, 40 + ∠x + 25 = 180o … [∵angles on straight line]

65 + ∠x = 180o

∠x = 180o – 65

∴ ∠x = 115o

 

(i) If two angles are complementary, then the sum of their measures is 90o.

(ii) If two angles are supplementary, then the sum of their measures is 180o.

(iii) Two angles forming a linear pair are supplementary.

(iv) If two adjacent angles are supplementary, they form a linear pair.

(v) If two lines intersect at a point, then the vertically opposite angles are always equal.

(vi) If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are obtuse angles.

(i) Two angles are said to be supplementary if the sum of their measures is 180o.

The given angle is 105o

Let the measure of its supplement be xo.

Then,

= x + 105o = 180o

= x = 180o – 105o

= x = 75o

Hence, the supplement of the given angle measures 75o.

(ii) Two angles are said to be supplementary if the sum of their measures is 180o.

The given angle is 87o

Let the measure of its supplement be xo.

Then,

= x + 87o = 180o

= x = 180o – 87o

= x = 93o

Hence, the supplement of the given angle measures 93o.

(iii) Two angles are said to be supplementary if the sum of their measures is 180o.

The given angle is 154o

Let the measure of its supplement be xo.

Then,

= x + 154o = 180o

= x = 180o – 154o

= x = 26o

Hence, the supplement of the given angle measures 93o.

 

(i) ∠AOD and ∠BOC are obtuse vertically opposite angles in the given figure.

(ii) ∠EOA and ∠AOB are adjacent complementary angles in the given figure.

(iii) ∠EOB and EOD are the equal supplementary angles in the given figure.

(iv) ∠EOA and ∠EOC are the unequal supplementary angles in the given figure.

(v) ∠AOB and ∠AOE, ∠AOE and ∠EOD, ∠EOD and ∠COD are the adjacent angles that do not form a linear pair in the given figure.

 

(i) By observing the figure, we came to conclude that,

Yes, as ∠1 and ∠2 have a common vertex, i.e., O and a common arm, OC.

Their non-common arms, OA and OE, are on both sides of the common arm.

(ii) By observing the figure, we came to conclude that,

No, since they have a common vertex O and common arm OA.

But, they have no non-common arms on both sides of the common arm.

(iii) By observing the figure, we came to conclude that,

Yes, as ∠COE and ∠EOD have a common vertex, i.e. O and a common arm OE.

Their non-common arms, OC and OD, are on both sides of the common arm.

(iv) By observing the figure, we came to conclude that,

Yes, as ∠BOD and ∠DOA have a common vertex, i.e. O and a common arm OE.

Their non-common arms, OA and OB, are opposite to each other.

(v) Yes, ∠1 and ∠2 are formed by the intersection of two straight lines AB and CD.

(vi) ∠COB is the vertically opposite angle of ∠5. Because these two angles are formed by the intersection of two straight lines AB and CD.

 

By observing the figure,

∠d = ∠125o … [∵ corresponding angles]

We know that Linear pair is the sum of adjacent angles is 180o

Then,

= ∠e + 125o = 180o … [Linear pair]

= ∠e = 180o – 125o

= ∠e = 55o

From the rule of vertically opposite angles,

∠f = ∠e = 55o

∠b = ∠d = 125o

By the property of corresponding angles,

∠c = ∠f = 55o

∠a = ∠e = 55o

 

(i) Let us assume the other angle on the line m be ∠y,

Then,

By the property of corresponding angles,

∠y = 110o

We know that Linear pair is the sum of adjacent angles is 180o

Then,

= ∠x + ∠y = 180o

= ∠x + 110o = 180o

= ∠x = 180o – 110o

= ∠x = 70o

(ii) By the property of corresponding angles,

∠x = 100o

 

(i) Let us consider AB ∥ DG.

BC is the transversal line intersecting AB and DG.

By the property of corresponding angles

∠DGC = ∠ABC

Then,

∠DGC = 70o

(ii) Let us consider BC ∥ EF.

DE is the transversal line intersecting BC and EF.

By the property of corresponding angles

∠DEF = ∠DGC

Then,

∠DEF = 70o

 

(i) Corresponding angles property is used in the above statement.

(ii) Alternate interior angles property is used in the above statement.

(iii) Interior angles on the same side of the transversal are supplementary.

 

(i) By observing the figure, the pairs of the corresponding angles are

∠1 and ∠5, ∠4 and ∠8, ∠2 and ∠6, ∠3 and ∠7

(ii) By observing the figure, the pairs of alternate interior angles are

∠2 and ∠8, ∠3 and ∠5

(iii) By observing the figure, the pairs of interior angles on the same side of the transversal are ∠2 and ∠5, ∠3 and ∠8.

(iv) By observing the figure, the vertically opposite angles are,

∠1 and ∠3, ∠5 and ∠7, ∠2 and ∠4, ∠6 and ∠8

 

(i) Let us consider the two lines, l and m.

n is the transversal line intersecting l and m.

We know that the sum of interior angles on the same side of the transversal is 180o.

Then,

= 126o + 44o

= 170o

But, the sum of interior angles on the same side of transversal is not equal to 180o.

So, line l is not parallel to line m.

(ii) Let us assume ∠x be the vertically opposite angle formed due to the intersection of the straight line l and transversal n,

Then, ∠x = 75o

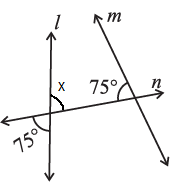
Let us consider the two lines, l and m.

n is the transversal line intersecting l and m.

We know that the sum of interior angles on the same side of the transversal is 180o.

Then,

= 75o + 75o

= 150o

But, the sum of interior angles on the same side of transversal is not equal to 180o.

So, line l is not parallel to line m.

(iii) Let us assume ∠x be the vertically opposite angle formed due to the intersection of the Straight line l and transversal line n.

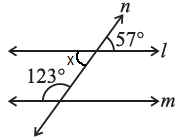
Let us consider the two lines, l and m.

n is the transversal line intersecting l and m.

We know that the sum of interior angles on the same side of the transversal is 180o.

Then,

= 123o + ∠x

= 123o + 57o

= 180o

∴ The sum of interior angles on the same side of the transversal is equal to 180o.

So, line l is parallel to line m.

(iv) Let us assume ∠x be the angle formed due to the intersection of the Straight line l and transversal line n.

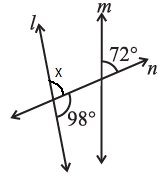
We know that the Linear pair is the sum of adjacent angles equal to 180o.

= ∠x + 98o = 180o

= ∠x = 180o – 98o

= ∠x = 82o

Now, we consider ∠x and 72o are the corresponding angles.

For l and m to be parallel to each other, corresponding angles should be equal.

But, in the given figure, corresponding angles measure 82o and 72o, respectively.

∴ Line l is not parallel to line m.