Mathematical strategies applied to manage numbers with both real and imaginary components are complex number formulas. Expressing a complex number as \( z = a + bi \), \( a \) is the real component; \( b \) is the imaginary part; \( i \) is the imaginary unit with condition \( i^2 = -1 \). These equations let you add, subtract, multiply, divide complicated numbers. Two complex numbers, for instance, multiply using the formula \( (a + bi) \times (c + di) = (ac - bd) + (ad +bc)i \).

Their formulas and complex numbers have broad uses in many different disciplines. In electrical engineering, they examine signal processing and alternating current (AC) circuits. They assist to explain quantum mechanics and wave events in physics. Moreover, in advanced mathematics especially in functions and equations involving polynomials and differential equations, complex numbers are basic. Their capacity to represent and control two-dimensional quantities makes them rather helpful for addressing issues where conventional real-number computation falls short.

Complex Number Visual:

 

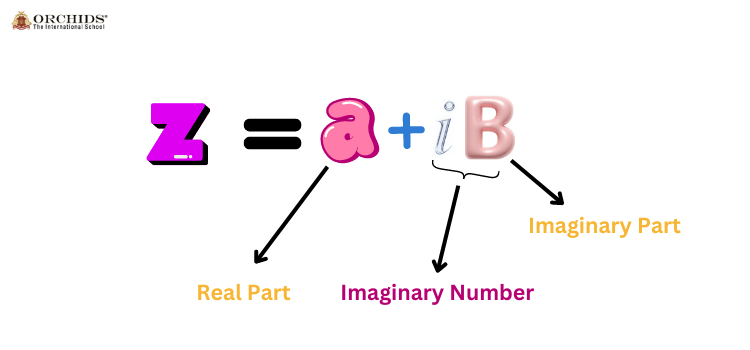
Complex numbers are numbers that have both a real part and an imaginary part. Here are some key formulas related to complex numbers:

Standard Form Complex Number: 

          z=a+bi

• $a$ is the real part.
• $b$ is the imaginary part.
• $i$ is the imaginary unit, where i2=−1i^2 = -1i2=−1.

Addition and Subtraction Complex Number:

• • $(a+bi)+(c+di)=(a+c)+(b+d)i$
  • (a+bi)−(c+di)=(a−c)+(b−d)i

Multiplication Complex Number:

(a+bi)×(c+di)=(ac−bd)+(ad+bc)i

Division Complex Number:

Conjugate Complex Number:

The conjugate of $a+bi$ is $a-bi$.

Modulus Complex Number:

​

Argument Complex Number:

Polar Form Complex Number:

These formulas are essential for manipulating and understanding complex numbers in various mathematical and engineering contexts.

Complex Number Examples

Other Related Sections

NCERT Solutions | Sample Papers | CBSE SYLLABUS| Calculators | Converters | Stories For Kids | Poems for Kids| Learning Concepts | Practice Worksheets | Formulas | Blogs | Parent Resource