The pattern in Maths for Class 5

1) Find the Missing Numbers in the Given Series:

21,34,55,,89,144,_____,_____,______,987.

Each term is the sum of the two preceding terms in the given series.
The first missing term is:

The first missing term is:
89 + 144 = 233
The second missing term is:
144 + 233 = 377
The third missing term is:
233 + 377 = 610
Therefore, the complete series is:

21,34,55,,89,144,233,377,610,987.

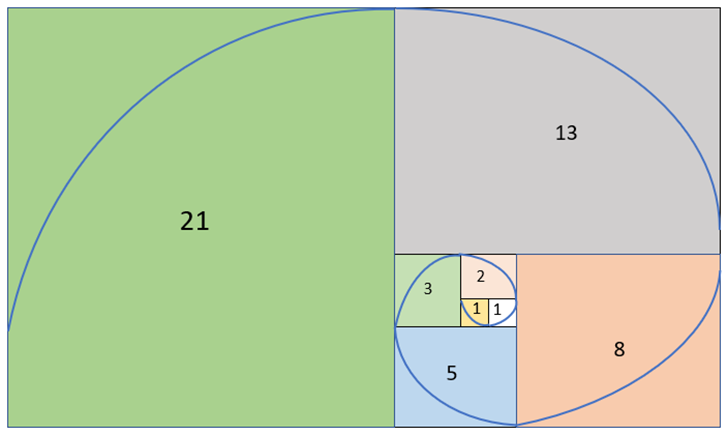
2) Draw a Golden Spiral for the Fibonacci Numbers:
1, 1, 2, 3, 5, 8, 13, 21.

The Golden Spiral for the Fibonacci Numbers 1, 1, 2, 3, 5, 8, 13, and 21 are shown below.

3) Write the Length of the Side of Each Square if the Given Figure Follows the Golden Curve.

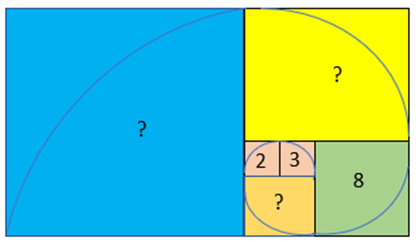
The given figure follows the Fibonacci sequence.
The side of the orange square should be:
2 + 3 = 5
The side of the yellow square should be:
5 + 8 = 13
The side of the blue square should be:
8 + 13 = 21
The complete figure is

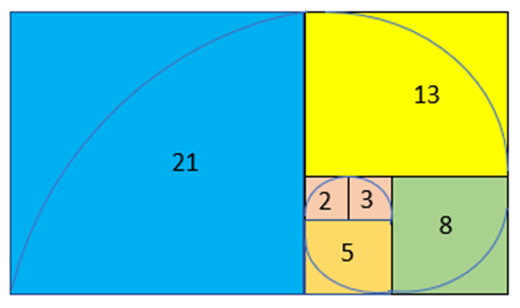
4) Find the Difference Between the Area of the Blue Square and the Yellow Square.

Step 1: The formula to calculate the area of the square is
Area = Side × Side
The side of the blue square is 8.
Area of the blue square = 8 × 8
= 64 square unit

Step 2:

The side of the yellow square is 5.
Area of the yellow square = 5 × 5
= 25 square unit

Step 3:

The difference in the area = 64 – 25
= 39 square unit

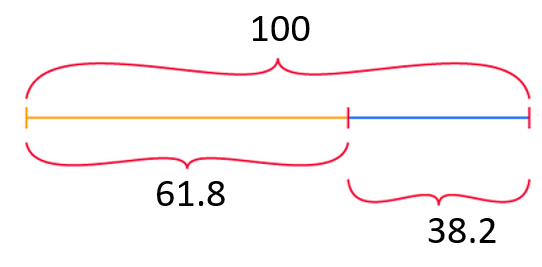
5) Divide 100 Into Two Parts Such That It Follows the Golden Ratio.

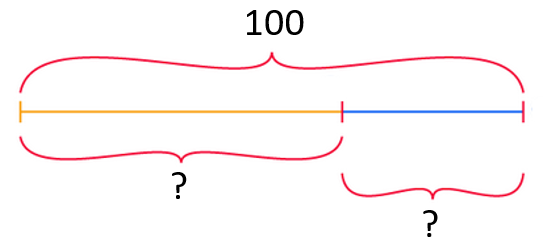
To follow the Golden ratio, the two parts should be such that the ratio of the bigger to the smaller part should equal 100 to the larger part.

The correct answer is 61.8 + 38.2 = 100.

6) Give an Example of a Rectangle That Follows the Golden Ratio.

The rectangle with a Golden ratio should be a combination of a square and a rectangle with the dimension of Fibonacci numbers.

One such example is the combination of the square of side 34 units and a rectangle of dimensions 55 units and 34 units.

Ratio = 55/34= 1.61764…. = 1.618 89/55= 1.61818181…. = 1.618

Thus, one example of a Fibonacci rectangle is a rectangle of length 89 units and width 34unitst.

7) Complete the Right Side of the Pattern Following the Golden Curve.

The complete pattern is shown below: