Admissions Open for 2025-26
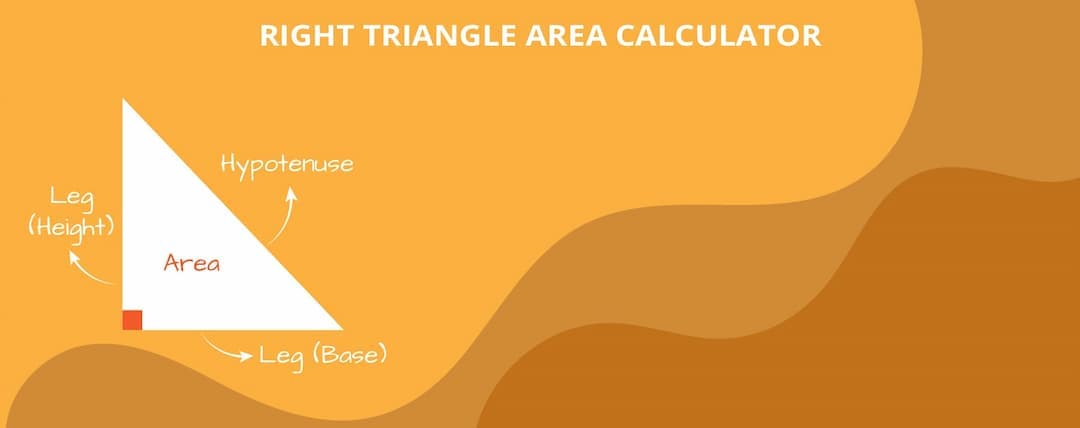
Right Triangle Area Calculator
A right triangle is a fundamental geometric shape characterized by one angle measuring 90 degrees. The area of a right triangle, a measure of its surface enclosed within its three sides, is pivotal in various fields, including mathematics, engineering, and architecture. Calculating this area is crucial for tasks such as determining land measurements, constructing buildings, and solving geometry problems.
What is the Right Triangle Area ?
The area of a right triangle is the amount of surface that the triangle covers. It is measured in square units, such as square inches, square centimeters, or square meters.
Why to use the Right Triangle Area Calculator?
A Right Triangle Area Calculator simplifies the tedious manual calculation process. It provides quick and accurate results, saving time and effort, especially in scenarios requiring multiple calculations or when precision is paramount.
When to use the Right Triangle Area Calculator?
This calculator is utilized whenever there's a need to determine the area of a right triangle, whether for academic assignments, architectural blueprints, or land surveying. It streamlines the process, making it efficient and error-free.
Where to use the Right Triangle Area Calculator?
Right Triangle Area Calculators find applications in various fields such as construction, engineering, physics, and geometry. Whether in classrooms, construction sites, or research laboratories, this tool proves invaluable for professionals and students alike.
The formula to calculate the area of a right triangle is:
Examples:
Base = 6 units
Height = 4 units
Area = 12 units 2
Base = 8 units
Height = 10 units
Area = 40 units 2
Base = 12 units
Height = 9 units
Area = 54 units 2
Frequently Asked Questions
No, this calculator is specifically designed for right triangles. For other types of triangles, different formulas apply.
If you know the lengths of the two sides forming the right angle, you can use trigonometric functions such as sine, cosine, or tangent to find the height.
No, the order doesn't matter as long as you correctly input the values for the base and height.