Admissions Open for 2025-26
Diagonal of Rectangle Calculator
Diagonal of Rectangle Calculator, a valuable tool for anyone exploring the dimensions of rectangles. Discover how to find the diagonal of a rectangle effortlessly with our user-friendly calculator, designed to simplify your mathematical tasks.
What is the Diagonal of a Rectangle ?
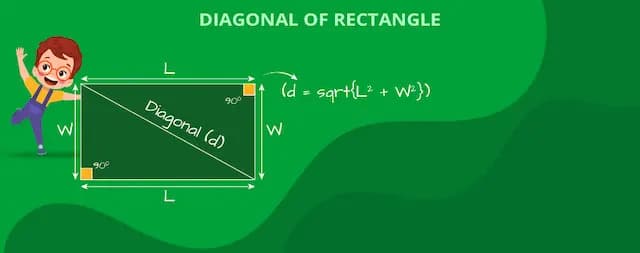
The diagonal of a rectangle is the line segment connecting opposite corners or vertices. It is longer than the sides and can be calculated using the Pythagorean theorem
Why Calculate Rectangle Diagonal Calculator?
Calculating the diagonal of a rectangle helps determine the distance between opposite corners, providing a key measurement in geometry and design.
When to Use Rectangle Diagonal Calculator ?
Use the diagonal length when designing structures, determining diagonal bracing, or ensuring accurate measurements for square footage in construction and architecture.
How to Calculate Diagonal of a Rectangle?
To calculate the diagonal of a rectangle, use the formula (d = sqrt(l2 + w2) ) or utilize an online calculator for quick and accurate results.
Formula:The Diagonal of a Rectangle (d) can be calculated using the Pythagorean Theorem:
d =
Where
l is the length of rectangle
w is the width of rectangle
Examples
For a rectangle with length (l = 6) units and width (w = 8) units,
Solution:
Using the formula d =
d =
d =
d = 10 units
For a rectangle with length (l = 10) units and the diagonal is (d = 13) units.
Solution:
Using the formula w =
w =
w =
w = 8.30 units
For a rectangle with diagonal is (d = 15) units, and the width is (w = 9) units
Solution:
Using the formula l =
l =
l =
l = 12 units
Frequently Asked Questions
Yes, if the rectangle is a square, the diagonal equals the square root of twice the side length, confirming its square nature.
Diagonal measurements influence spatial aesthetics, aiding in optimal furniture placement and enhancing room design.
Yes, diagonal measurements are crucial in construction, influencing material estimates and overall project costs.