Admissions Open for 2025-26
Semi-Circle Area Calculator
A Semicircle is half of a circle, and calculating its area involves understanding its properties and using the appropriate formula. The area of a semicircle is an important concept in geometry and is often encountered in mathematics and engineering studies.
A Semicircle is half of a circle, and calculating its area involves understanding its properties and using the appropriate formula. The area of a semicircle is an important concept in geometry and is often encountered in mathematics and engineering studies. .
What is a Semicircle Area Calculator ?
A Semicircle Area Calculator is a tool designed to quickly and accurately compute the area of a semicircle when its radius or diameter is provided. It simplifies the process of manually applying the area formula, making it convenient for students, professionals, and anyone in need of this calculation. ?
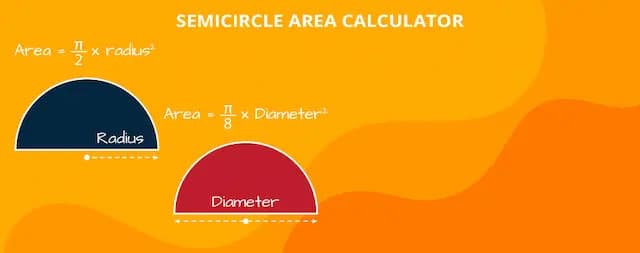
How to calculate the Area of Semicircle ?
Using Radius:
The area (A) of a semicircle with radius (r) can be calculated using the formula:
Using Diameter:
Alternatively, if the diameter (d) is known, the area can be calculated as:
Examples:
Given radius, r = 7 cm
Using the formula:
Area = 76.97 cm2
Given radius, r = 5 cm
Using the formula:
Area = 39.26 cm2
Given diameter, d = 10
Using the formula:
Area = 39.26 cm2
Frequently Asked Questions
The Semicircle Area Calculator provides accurate results based on the input radius or diameter.
The calculator allows input in various units like centimeters, meters, inches, etc., and returns the area in the corresponding square units.
The calculator is designed with a user-friendly interface, making it simple and intuitive to input the required values and obtain the area of the semicircle.