HCF Questions & Answers

Solving HCF questions is crucial for students of all grades. It is one of the most important concepts to learn for various competitive exams like Olympiads. Understanding different methods used to find the highest common prime factor, like the shortcut method and prime factorisation, is important. By practising HCF questions, students can gain conceptual fluency of the topic along with speed and clarity in calculations.

Table of Contents

• What is HCF?
• How to Calculate the HCF?
• Sample HCF Questions
• Applications of HCF Concepts
• Frequently Asked Questions

What is HCF?

HCF (Highest Common Factor) is the greatest number that divides the given set of two or more numbers. In other words, HCF is the product of the smallest power of each common prime factor in the numbers. The HCF of any given numbers can be calculated using different methods, such as factorisation, division, long division, and the shortcut method.

How to Calculate the HCF?

In order to solve HCF questions, we can apply different methods of calculating HCF. Below are the three methods used most commonly to find HCF:

The above-stated methods of finding HCF will make it easy for you to solve all types of HCF questions, whether small or large numbers.

Sample HCF Questions

Example 1: What is the HCF of 24 and 36?

Solution: 

1. First, list-down the factors of number 24, i.e., 1, 2, 3, 4, 6, 8, 12, 24

2. List-down the factors of number 36: 1, 2, 3, 4, 6, 9, 12, 18, 36

3. Identify the highest common factor: 12

HCF = 12

Example 2: Find the HCF of 135 and 225 using prime factorisation.

Solution:

1. First, let’s find the prime factors of 135, i.e., 3 × 3 × 3 × 5

2. Now, find the prime factors of 225, i.e., 3 × 3 × 5 × 5

3. The common prime factors are 3 × 3 × 5 = 45

Final Answer: HCF = 45

Example 3: What is the highest common factor of 96 and 404?

Solution: 

1. Write the prime factors of 96 = 2 × 2 × 2 × 2 × 2 × 3 = 25 × 3

2. Write the prime factors of 404 = 2 × 2 × 101 = 22 × 101

HCF(96, 404) = 2 x 2 = 4

Example 4: If the HCF of two numbers is 29 and their sum is 174, what will be the value of the numbers? 

Solution:

Given that the HCF of two numbers is 29.

Let 29a and 29b be the two required numbers.

According to the given,

29a + 29b = 174

29(a + b) = 174

a + b = 174/29 = 6

The pair of coprime values with sum 6 is (1, 5).

So, the possible numbers are 29 x 1 = 29

29 x 5 = 145

Verification:

Sum of numbers = 29 + 145 = 174

Hence, the required numbers are 29 and 145.

Example 5: Find the highest common factor of the fractions 2/3 & 5/8.

Solution: Formula to find the HCF of Fractions = HCF of numerator / LCM of denominator

For the given fractions, 2/3 & 5/8, the numerators are 2 & 5, while the denominators are 3 & 8.

The first step is to find the HCF of the numerator (2, 5) = 1

LCM of the numerator (3, 8) = 24

Therefore, the HCF of 2/3 and 5/8 is 1/24. 

Example 6: There are two wires of length 30 cm and 60 cm. If the wire is to be cut into equal pieces, what will be the length of each piece?

Solution: HCF of 30 and 60.

30 = 2 × 3 × 5

60 = 2 × 2 × 3 × 5 

Common factors: 2 × 3 × 5 = 30

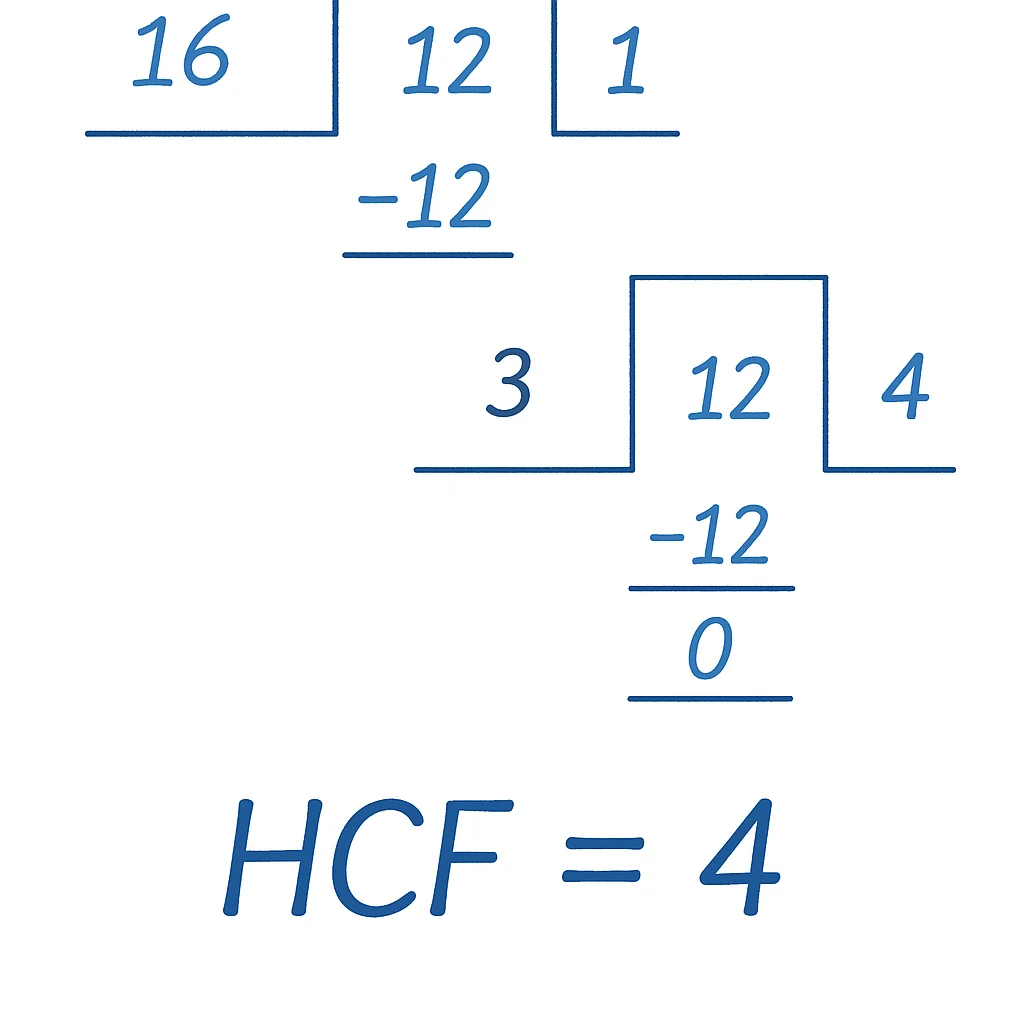
Example 7: Find the HCF of 16 and 12 using the division method.

Solution: The HCF of 16 and 12 can be found using the division method as follows:

 

Applications of HCF Concepts

The concept of HCF questions is used in various fields such as packaging, dividing things evenly, designing timetables, or even in banking systems. Learning these skills will help you to apply math far beyond exams. Practising the HCF questions with our worksheets will not only help you gain an in-depth understanding of the concepts but will also enable you to build a solid foundation for high-level competitive exams.

Frequently Asked Questions

1. What is HCF?

Answer: The highest common factor of a given set of numbers is defined as the highest number that can divide each number in the set.

2. What are the various methods used to find the HCF?

Answer: Prime factorisation, division, long division, and the shortcut method are some of the methods used to find the HCF.

3. List the steps to calculate the HCF of three numbers.

Answer: The step-by-step process to find the HCF of three numbers is listed below:
1. Calculate the HCF of the 1st two numbers given in the question.
2. Then, calculate the HCF of the third number and the answer derived from the above step.
3. The HCF of the given three numbers is the number obtained from step 2.