What Is Polyhedron?
We know that each three-dimensional shape has faces, edges, and vertices.
Faces: A flat surface.
Edges: A point where two faces meet each other.
Vertices: A corner where edges meet.
A three-dimensional shape
which has sharp vertices, flat polygonal faces,
and straight edges is called a polyhedron.
1) What Are the Types of Polyhedrons?
There are two types of polyhedrons, namely:
- Convex polyhedron
- Concave polyhedron
2) What is Convex Polyhedron?
A polyhedron whose faces, edges and vertices do not intersect each other is called a convex polyhedron.
Example:
3) What is a Concave Polyhedron?
A polyhedron whose faces, edges and vertices intersect is called a concave polyhedron.
Example:
Regular Polyhedron
A regular polyhedron is made of regular polygons that meet on a vertex keeping the number of faces the same.
| Shapes Name | Shape Figure | Faces |
|---|---|---|
| 1. Cube |
 |
6 square faces |
| 2. Tetrahedron |
 |
4 equilateral triangular faces |
| 3. Octahedron |
 |
8 equilateral triangular faces |
| 4. Dodecahedron |
 |
12 pentagonal faces |
| 5. Icosahedron |
 |
20 equilateral triangular faces |
4) How Many Faces Does a Dodecahedron Have?
A regular dodecahedron is made of 12 pentagonal faces.
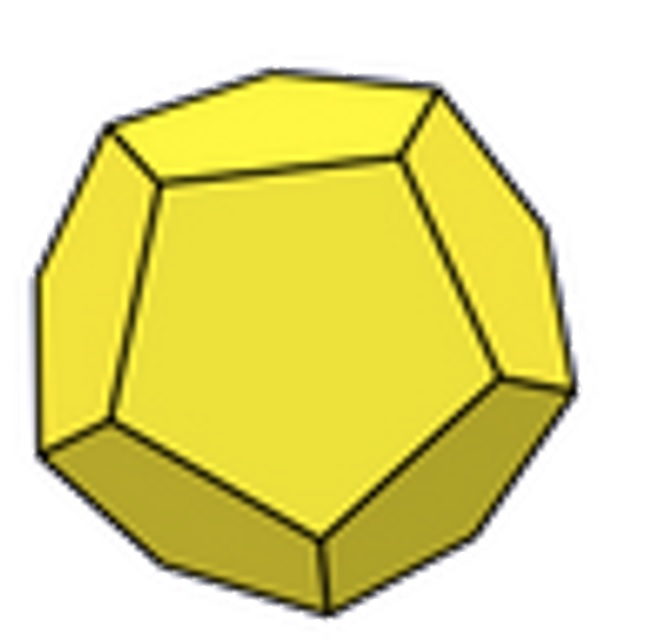
5) Name the Regular Polyhedron With a Square Face.
A cube has 4 square faces.
Euler’s Formula:
According to Euler’s Formula, for any convex polyhedron, we have,
F + V – E = 2, where
F = Number of faces.
V = Number of vertices.
E = Number of edges.
Also, from Euler’s Formula, we get,
E = F + V – 2
F = 2 + E – V
V = 2 + E – F
Number Operations
6) What Is the Difference Between the Regular Octahedron and the Tetrahedron?
A regular octahedron comprises eight equilateral triangular faces, and a regular tetrahedron has four equilateral triangular faces.
7) The Dodecahedron Has 20 Vertex Corners and 30 Edges. Find the Number of Faces It Has.
From Euler’s formula, we have F = 2 + E – V
Substitute 20 for V and 30 for E in the formula F = 2 + E – V and then simplify to get the number of faces of the Dodecahedron.
F = 2 + 30 – 20
= 32 – 20
= 12
Therefore, Dodecahedron has 12 faces.
8) Name the Regular Polyhedron, Which Has 20 Triangular Faces.
A regular polyhedron that has 20 equilateral triangular faces is called an icosahedron.
9) The Icosahedron Has 20 Triangular Faces and 30 Edges. Find the Number of Vertices It Has.
From Euler’s formula, we have V = 2 + E – F
Substitute 20 for F and 30 for E in the formula V = 2 + E – F and then simplify to get the number of vertices of the Icosahedron.
V = 2 + 30 – 20
= 32 – 20
= 12
Therefore, Icosahedron has 12 vertices.
10) The Dodecahedron Has 20 Vertex Corners and 30 Edges. Find the Number of Faces It Has.
From Euler’s formula, we have F = 2 + E – V
Substitute 20 for V and 30 for E in the formula F = 2 + E – V and then simplify to get the number of faces of the Dodecahedron.
F = 2 + 30 – 20
= 32 – 20
= 12
Therefore, Dodecahedron has 12 faces.
11) The Octahedron Has 6 Vertex Corners and 8 Faces. Find the Number of Edges It Has.
From Euler’s formula, we have E = F + V – 2.
Substitute 8 for F and 6 for V in the formula E = F + V – 2 and then simplify to get the number of edges of the Octahedron.
E = 8 + 6 – 2
= 14 – 2
= 12
Therefore, Octahedron has 12 edges.