Isosceles Triangle | Properties, Formula & Examples

An isosceles triangle is a triangle that has two equal sides. Based on the length of the sides, a triangle can be classified into three different types: equilateral triangle (equal sides), isosceles and scalene triangles. An equilateral triangle is a triangle with three equal sides, and a scalene triangle is a triangle with no equal sides.

A triangle is an important shape that holds relevance not only in mathematics but also in our lives, from construction to transportation. Therefore, learning and understanding the basic properties and applications of a triangle are highly important in our lives.

Table of Contents

• Define Isosceles Triangle
• Properties of an Isosceles Triangle
• Types of Isosceles Triangle
• Perimeter of an Isosceles Triangle
• Area of an Isosceles Triangle
• Important Formulas
• Frequently Asked Questions
• Sample Problems

Define Isosceles Triangle

The isosceles triangle is a type of triangle that has two equal sides, and the third side is known as a base. The angles opposite to the two equal sides are also equal. 

Types of Isosceles Triangle

• Two sides of this triangle are equal.

• Angles opposite to the equal sides are also equal.

• Its third side is known as the base.

• The sum of the angles of isosceles triangle is always 180°

Perimeter of an Isosceles Triangle

Based on the measure of the angle of an isosceles triangle, we can further classify them into the following:

I. Isosceles Acute Triangle 

II. Isosceles Obtuse Triangle

III. Isosceles Right Triangle

Types of Isosceles Triangle	Definition
Isosceles Acute Triangle	An acute isosceles triangle is a triangle with an acute angle between the two equal sides.
Isosceles Obtuse Triangle	If the angle between the two equal sides of an isosceles triangle is obtuse, then it is known as an obtuse isosceles triangle.
Isosceles Right Triangle	When the angle between two equal sides of a triangle is 90°, it is called an isosceles right triangle.

 

Perimeter of an Isosceles Triangle

The perimeter of an isosceles triangle is defined as the length of three sides denoted by 'P' and is equal to 2a + b, where 'a' is the length of the two equal sides and 'b' is the length of the base. P = 2a + b

Area of an Isosceles Triangle

The area of an isosceles triangle is defined as the total amount of area enclosed within its boundary. It is calculated using the formula Area = ½ x base x height. The units of measuring area is always square centimetres, meters, inches, foot, etc.

Important Formulas

It is important to memorise some of the important formulas used to calculate various dimensions of an isosceles triangle. These formulas are listed below:

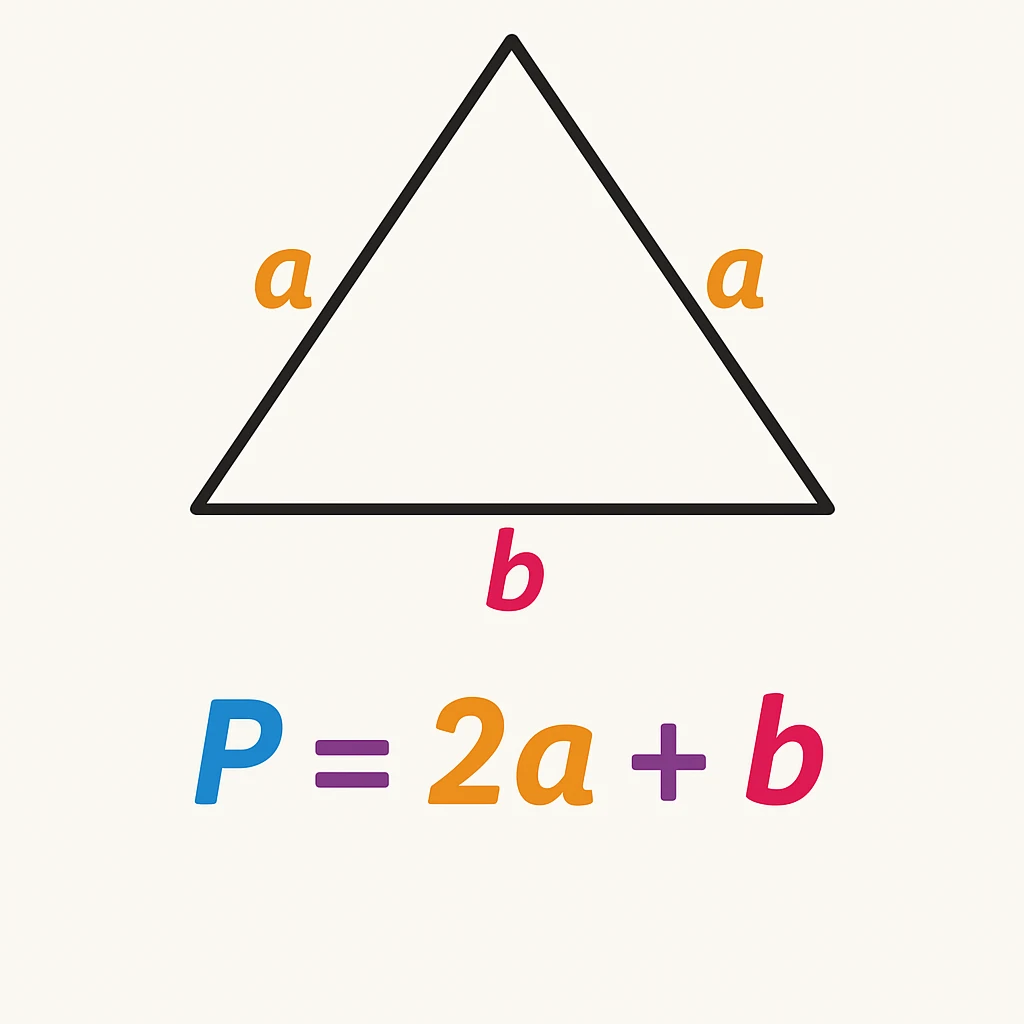
The isosceles triangle is among one of the most basic structures used in engineering, architecture, design, construction, and so much more. It is one of the most reliable structures based on its strength and properties. Some of the main examples of isosceles triangles are roofs and supportive structures in bridges.

Solved Example on Isosceles Triangle

Example: Find the area of an isosceles triangle if the height is 4 cm and the base is 5 cm.

Solution: Given that,

Base = 5 cm and height = 4 cm

We know that the area of an isosceles triangle is ½ × b × h square units

Now, substitute the base and height values in the formula

The area of an isosceles triangle is ½ × b × h

A = ½ × 5 × 4 = 10 cm²

Example: Find the perimeter of a triangle with equal sides measuring to 5 cm and base measuring as 4 cm.

Solution: Given: Base = 4 cm

Length of the two equal arms = 5 cm

We know that the formula to calculate the perimeter of an isosceles triangle is  P = 2a + b units

Now, substitute the values in the perimeter formula; we get

P = 2(5) + 4 = 10 + 4 = 14 cm

Hence, the perimeter of an isosceles triangle is 14 cm. 

Frequently Asked Questions

1. What is an isosceles triangle?

Answer: A triangle with two equal sides is called an isosceles triangle.

2. What are the properties of an isosceles triangle?

Answer: Properties of an isolated triangle are listed as under:

• Two sides of this triangle are equal.

• Angles opposite to the equal sides are also equal.

• Its third side is known as the base.

• The sum of the angles of isosceles triangle is always 180°
  
  

3. How to find the area and perimeter of an isosceles triangle?

Answer: The formulas used to find the area and perimeter of an isosceles triangle are:

 Area = ½ x base  x height and Perimeter P = 2a + b

4. What is a scalene triangle?

Answer: A triangle is said to be a scalene triangle when none of its sides are equal to each other.