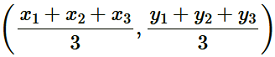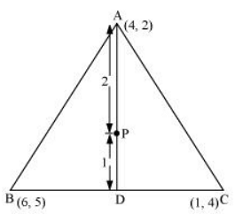
(i) Median AD of the triangle will divide the side BC in two equal parts.
Therefore, D is the mid-point of side BC
Coordinate of D = (6 +1/2, 5 + 4/2) =(7/2,9/2)
(ii) Point P divides the side AD in a ratio 2:1.
Coordinate of P = 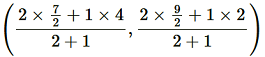 = (11/3 , 11/3)
= (11/3 , 11/3)
(iii) Median BE of the triangle will divide the side AC in two equal parts.
Therefore, E is the mid-point of side AC.
Coordinate of E = (4+1/2, 2+4/2) = (5/2,3)
Point Q divides the side BE in a ratio 2:1.
Coordinate of Q =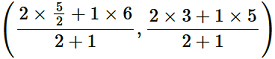 = (11/3 , 11/3)
= (11/3 , 11/3)
Median CF of the triangle will divide the side AB in two equal parts. Therefore, F is the mid-point of side AB
Coordinate of F = (4+6/2, 2+5/2) = (5,7/2)
Point R divides the side CF in a ratio 2:1.
Coordinate of R =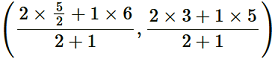 = (11/3 , 11/3)
= (11/3 , 11/3)
(iv) It can be observed that the coordinates of point P, Q, R are the same.
Therefore, all these are representing the same point on the plane i.e., the centroid of the triangle.
(v) Consider a triangle, ΔABC, having its vertices as A(x1,y1), B(x2,y2) and C(x3,y3)
Median AD of the triangle will divide the side BC in two equal parts. Therefore, D is the mid-point of side BC.
Coordinate of D =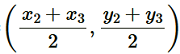
Let the centroid of this triangle be O.
Point O divides the side AD in a ratio 2:1.
Coordinate of O =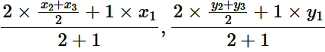
=