NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry

Given: A triangle ABC in which

B =90

We know that sin A = BC/AC = 3/4
Let BC be 3k and AC will be 4k where k is a positive real number.
By Pythagoras theorem we get,
AC2 = AB2 + BC2
(4k)2 = AB2 + (3k)2
16k2 - 9k2 = AB2
AB2 = 7k2
AB = √7 k
cos A = AB/AC = √7 k/4k = √7/4
tan A = BC/AB = 3k/√7 k = 3/√7

 

cosA=cos

 

Consider a triangle ABC in which

Let AB = 12k and AC = 13k

Then, using Pythagoras theorem,

(AC)2 = (AB)2 + (BC)2

(13 k)2 = (12 k)2 + (BC)2

169 k2 = 144 k2 + BC2

25 k2 = BC2

BC = 5 k

 (I)   Sin =

= =

(ii) Cos θ =

=   =

(iii)Tan θ =

 

= =

(iv) Cot θ =

= =

(v) Cosec θ =

= =

 

Let us draw a right angled triangle ABC, right angled at B.

Using Pythagoras theorem,

(i)

(ii)

,

 

Let ΔABC be a right-angled triangle, right-angled at B.
We know that cot A = AB/BC = 8/15   (Given)
Let AB be 8k and BC will be 15k where k is a positive real number.
By Pythagoras theorem we get,
AC2 = AB2 + BC2
AC2 = (8k)2 + (15k)2
AC2 = 64k2 + 225k2
AC2 = 289k2
AC = 17 k
sin A = BC/AC = 15k/17k = 15/17
sec A = AC/AB = 17k/8 k = 17/8

 

Consider a triangle ABC 

 

 

 

(i) sin 60° cos 30° + sin 30° cos 60°

(ii) 2 tan245° + cos230° – sin260°

(iii) cos 45°/(sec 30° + cosec 30°) 

(iv) (sin 30° + tan 45° – cosec 60°)/(sec 30° + cos 60° + cot 45°)

(v) (5cos260° + 4sec230° - tan245°)/(sin230° + cos230°)

 

(i) 2tan 30°/1+tan230° =
(A) sin 60°   (B) cos 60°  (C) tan 60°  (D) sin 30°

=

(ii) 1-tan245°/1+tan245° =

(A) tan 90°   (B) 1    (C) sin 45°  (D) 0

(iii) sin 2A = 2 sin A is true when A =

(A) 0°    (B) 30°  (C) 45°          (D) 60°

(iv) 2tan30°/1-tan230° =

(A) cos 60°   (B) sin 60°  (C) tan 60°  (D) sin 30°

……….(i)

 

(i) False.
Let A = 30° and B = 60°, then
sin (A + B) = sin (30° + 60°) = sin 90° = 1 and,
sin A + sin B = sin 30° + sin 60°
= 1/2 + √3/2 = 1+√3/2

(ii) True.
sin 0° = 0
sin 30° = 1/2
sin 45° = 1/√2
sin 60° = √3/2
sin  90° = 1
Thus the value of sin θ increases as θ increases.

(iii) False.
cos 0° = 1
cos 30° = √3/2
cos 45° = 1/√2
cos 60° = 1/2
cos 90° = 0
Thus the value of cos θ decreases as θ increases.

(iv) True.
cot A = cos A/sin A
cot 0° = cos 0°/sin 0° = 1/0 = undefined.

 

 (ii)

 

 

Consider a triangle ABC AB=4cm, BC= 3cm

.

And

 

Consider a triangle ABC in which

.

(i) 

(ii) 

 

Given that, PR + QR = 25 , PQ = 5
Let PR be x.  ∴ QR = 25 - x
By Pythagoras theorem ,
PR2 = PQ2 + QR2
x2 = (5)2 + (25 - x)2
x2 = 25 + 625 + x2 - 50x
50x = 650
x = 13
∴ PR = 13 cm
QR = (25 - 13) cm = 12 cm
sin P = QR/PR = 12/13
cos P = PQ/PR = 5/13
tan P = QR/PQ = 12/5

 

i) False.
In ΔABC in which ∠B = 90º,
AB = 3, BC = 4 and AC = 5
Value of tan A = 4/3 which is greater than.
The triangle can be formed with sides equal to 3, 4 and hypotenuse = 5 as
it will follow the Pythagoras theorem.
AC2 = AB2 + BC2
52 = 32 + 42
25 = 9 + 16
25 = 25

(ii) True.
Let a ΔABC in which ∠B = 90º,AC be 12k and AB be 5k, where k is a positive real number.
By Pythagoras theorem we get,
AC2 = AB2 + BC2
(12k)2 = (5k)2 + BC2
BC2 + 25k2 = 144k2
BC2 = 119k2
Such a triangle is possible as it will follow the Pythagoras theorem.

(iii) False.
Abbreviation used for cosecant of angle A is cosec A.cos A is the abbreviation used for cosine of angle A.

(iv) False.
cot A is not the product of cot and A. It is the cotangent of ∠A.

(v) False.
sin θ = Height/Hypotenuse
We know that in a right angled triangle, Hypotenuse is the longest side.
∴ sin θ will always less than 1 and it can never be 4/3 for any value of θ.

 

 

sin 67° + cos 75°
= sin (90° - 23°) + cos (90° - 15°)
= cos 23° + sin 15°

 

tan A = cot B
⇒ tan A = tan (90° - B)
⇒ A = 90° - B
⇒ A + B = 90°

 

(i) sin 18°/cos 72°
= sin (90° - 18°) /cos 72°
= cos 72° /cos 72° = 1

(ii) tan 26°/cot 64°
= tan (90° - 36°)/cot 64°
= cot 64°/cot 64° = 1

(iii) cos 48° - sin 42°
= cos (90° - 42°) - sin 42°
= sin 42° - sin 42° = 0

(iv) cosec 31° - sec 59°
= cosec (90° - 59°) - sec 59°
= sec 59° - sec 59° = 0

 

(i) tan 48° tan 23° tan 42° tan 67°
= tan (90° - 42°) tan (90° - 67°) tan 42° tan 67°
= cot 42° cot 67° tan 42° tan 67°
= (cot 42° tan 42°) (cot 67° tan 67°) = 1×1 = 1

(ii) cos 38° cos 52° - sin 38° sin 52°
= cos (90° - 52°) cos (90°-38°) - sin 38° sin 52°
= sin 52° sin 38° - sin 38° sin 52° = 0

 

tan 2A = cot (A- 18°)
⇒ cot (90° - 2A) = cot (A -18°)
Equating angles,
⇒ 90° - 2A = A- 18° ⇒ 108° = 3A
⇒ A = 36°

 

sec 4A = cosec (A - 20°)
⇒ cosec (90° - 4A) = cosec (A - 20°)
Equating angles,
90° - 4A= A- 20°
⇒ 110° = 5A
⇒ A = 22°

 

 (i) (sin263° + sin227°)/(cos217° + cos273°)

(ii)  sin 25° cos 65° + cos 25° sin 65°

 

(i)  (i) 9 sec2A - 9 tan2A =

(A) 1             (B) 9    (C) 8            (D) 0 

(ii) (1 + tan θ + sec θ) (1 + cot θ - cosec θ)
(A) 0             (B) 1    (C) 2            (D) - 1

 

(iii) (secA + tanA) (1 - sinA) =
(A) secA       (B) sinA   (C) cosecA  (D) cosA

(iv) 1+tan2A/1+cot2A =
(A) sec2A      (B) -1  (C) cot2A            (D) tan2A

 

 

(i) (cosec θ - cot θ)2 = (1-cos θ)/(1+cos θ)

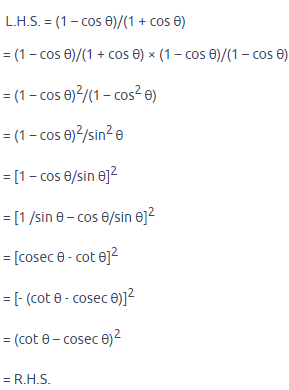
(ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A 

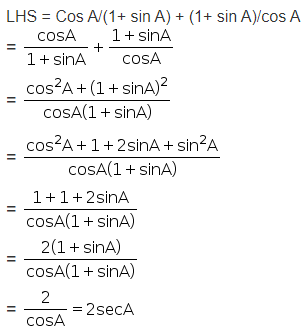
(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ

[Hint : Write the expression in terms of sin θ and cos θ]

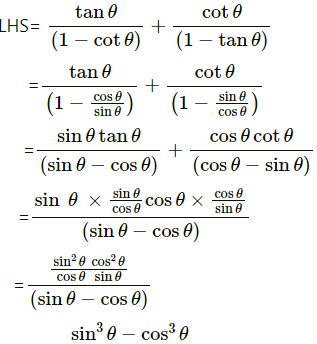
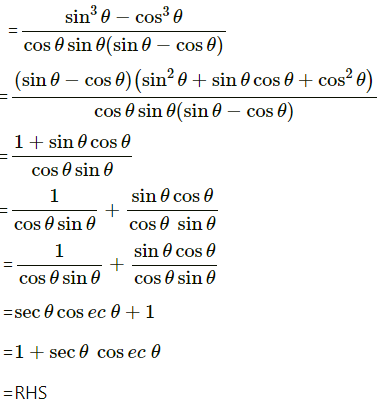
(iv) (1 + sec A)/sec A = sin2A/(1-cos A)  

[Hint : Simplify LHS and RHS separately] 

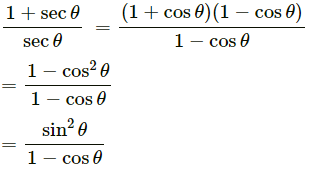
(v) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A,using the identity cosec2A = 1+cot2A

(vi) √1 + sin A/1 - sin A = sec A+ tan A

LHS = 1 + sin A/(1 - sin A) .....(1)

Multiplying and dividing by (1 + sin A)

⇒ (1 + sin A)(1 + sin A/1 - sin A)(1 + sin A)

= (1 + sin A)²/(1 - sin² A) [a² - b² = (a - b)(a + b)]

= (1 + sinA)/1 - sin² A

= 1 + sin A/cos² A

= 1 + sin A/cos A

= 1/cos A + sin A/cos A

= sec A + tan A

= R.H.S

(vii) (sin θ - 2sin3θ)/(2cos3θ-cos θ) = tan θ

(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7+tan2A+cot2A

(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)

 [Hint : Simplify LHS and RHS separately]

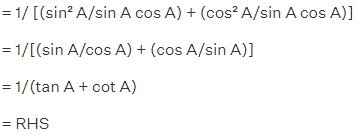
(x) (1+tan2A/1+cot2A) = (1-tan A/1-cot A)2 = tan2A