Curve

Introduction to Curve 

The curve is an important part of mathematics and forms the foundation for many concepts in geometry, calculus, and analytical geometry. The word 'curve' comes from the Latin 'curvus', which means 'bent' or 'curved'. Simply put, a curve is a smooth, continuous line that does not contain sharp corners.

Curves can take many shapes, such as straight lines, circles, parabolas, ellipses, and more. They are used to represent the relationship between variables, the path of moving objects, and real-life shapes like the arc of a bridge, the trajectory of a ball, or the outline of a leaf. Mathematically, curves are often represented by the use of equations in two or three dimensions.

In this article, we will learn about different types of curves, their equations, important properties, and how to analyse and plot them. With the examples of step-by-step solutions, this guide will clearly help you understand the curves and see their applications in mathematics and everyday life.

Table of Contents:

• Meaning
• Curve Shapes
• Types
• Simple Curve
• Non-Simple Curve
• Open Curve
• Closed Curve
• Upward Curve
• Downward Curve
• Curved Line
• Area Between Curves
• FAQs on Curve

Meaning

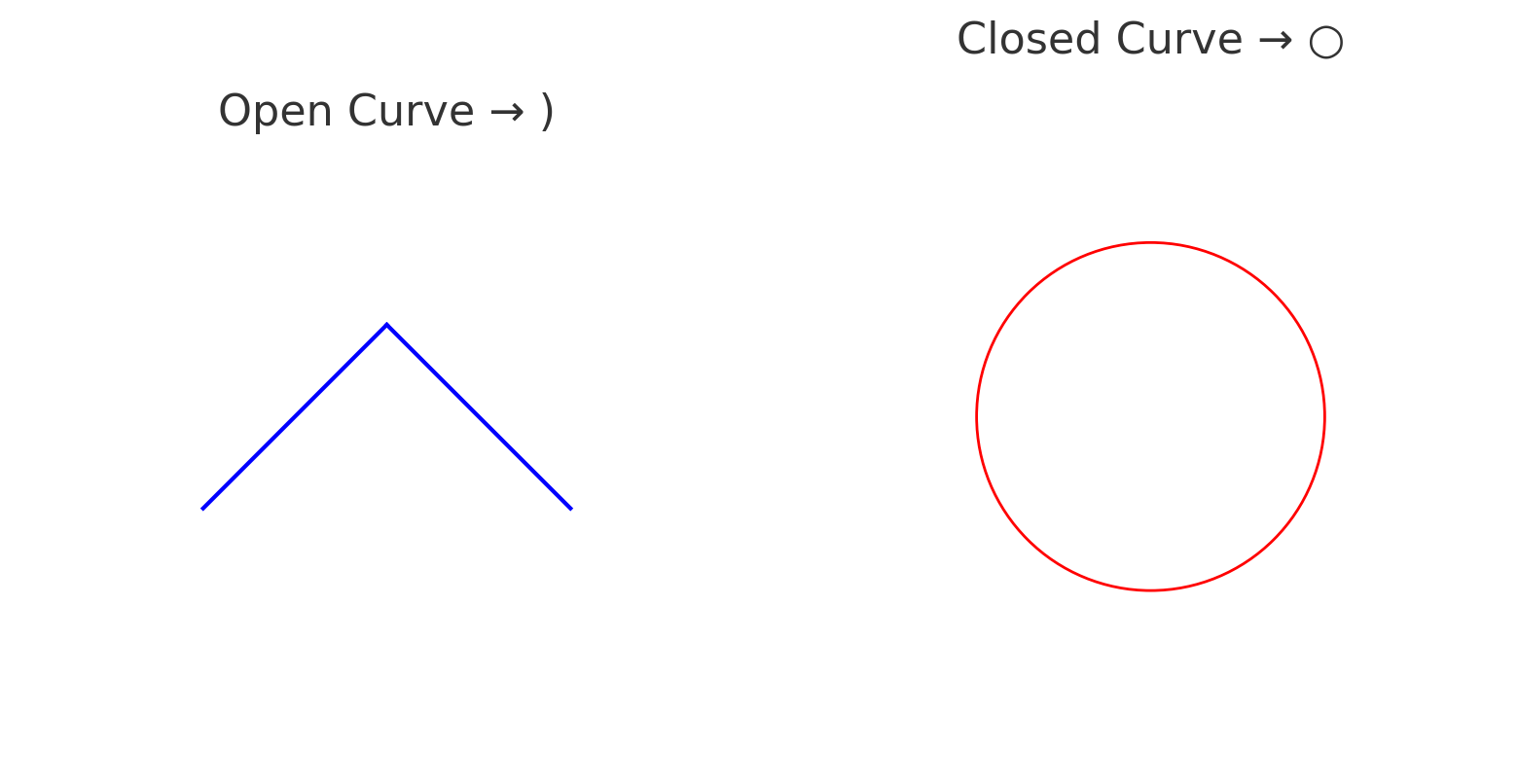
A curve is a smoothly flowing, continuous line that bends. It has no sharp edge or corner. To call a line a curve, the line must bend or change direction at least once.

• If the curve does not meet its starting point, it is called an open curve.

• If the curve meets at its starting point, it is called a closed curve.

Examples from daily life:

• The rainbow is an open curve in the sky.

• A circle drawn with a compass is a closed curve.

• The edge of a ball is also a curve.

Curve Shapes

Curves are found in both 2D shapes and 3D shapes.

• Two-Dimensional Curved Shapes

• Three-Dimensional Cured Shapes
  

1. Two-Dimensional Curved Shapes

These are flat shapes that we can draw on paper. Examples include:

• Circle: A perfectly round closed curve.

• Ellipse: Looks like a stretched circle.

• Parabola: A curve formed when something is thrown upwards and comes down.

• Hyperbola: An open curve with 2 separate parts.

• Arcs, Sectors, and Segments: Parts of a circle that are also curves.

2. Three-Dimensional Curved Shapes 

These are solid objects that take up space. Examples include:

• Sphere: like a ball, it has a curved surface everywhere.

• Cylinder: Like a can, with curved sides and 2 flat circles.

• Cone: Like an ice cream cone, with a curved side that comes to a point.
  
  

Types

A curve is a line that bends and changes direction. The curve is around us in nature, in the drawing, and in things we use every day. There are different types of curves. Let's learn about them one by one.

1. Simple Curve

A simple curve is a curve that bends smoothly but does not cross over itself.

• It can open or close.

• The main point is that the line never cuts off its own path.

Examples of real life:

• A circle was drawn on paper.

• A curved road that simply bends but does not loop back.

2. Non-Simple Curve

A non-simple curve is a curve that crosses itself. While bending, the line meets or is being cut by itself.

• This looks more complicated than a simple curve.

Examples of real life:

• The shape of a roller coaster loop.

• A figure "8" is made of one line.

3. Open Curve

An open curve has two ends. It does not include going back to the starting point.

• It looks like part of a bigger shape that has not been closed.

Examples of real life:

• A rainbow in the sky.

• A road that bends and keeps going.

4. Closed Curve

A closed curve joins back to its starting point and makes a complete shape.

• The closed curves form the boundary of 2D forms.

Examples of real life:

• A circle (like a coin).

• An ellipse (like a racing track).

5. Upward Curve

An upward curve bends upwards towards the top, such as the letter "U".

• It is wide at the top and narrow at the bottom.

• It looks like a smiling face.

Examples of real life:

• A curve of a bowl was placed on a table.

• Curve for a suspension bridge.

6. Downward Curve

A downward curve bends toward the down, such as the letter "n".

• It is wide at the bottom and narrow at the top

• It looks like a sad or scary face.

Examples of real life:

• A curve of an arch upside down.

• The top side of a hill.

Curved Line

A curved line is a line that is not straight but bent. If a line keeps turning and does not remain flat, we call that a curve. Most curves are smooth and continuous.

Curved line example in real life

We can see many curved lines around us:

• Turning part of a railway track.

• Loop of a roller coaster.

• The road bends on a hill.

• The shape of a rainbow in the sky.

In mathematics, we also see curved lines like:

• A parabola (U-shaped curve) is made from the graph of a quadratic equation.

• Ogive curve in statistics.

• The curved shape of an arrow.

Area Between Curves

The area tells us how much space is covered on the surface. When we talk about the area between two curves, it means the region lies between them.

To find this area in mathematics, we use the concept of integration. It's like adding very tiny slices of space to cover the total space.

Formula

If we have two curves, one f (x) and the other g (x), then the area between them from x = a to x = b:

A=∫ab[f(x)−g(x)]dx

Here:

• f (x) is a curve with a greater value (on top).

• g (x) is a curve of smaller value (below).

• a and b are early and outlet points.

Simple example:Think about the shape of a leaf. A leaf consists of two curved sides (up and down). The space inside those curves is the area between the curves.

FAQs on Curve

1. What is a curve in mathematics?

Answer: A curve is a line that bends smoothly without sharp corners. It can be open or closed.

2. What are the types of curves?

Answer: The main types of curves are straight line, open curve, closed curve, simple curve, and complex curve.

3. Is a straight line a curve?

Answer: In mathematics, even a straight line is considered the simplest form of a curve.

4. What is the difference between an open curve and a closed curve?

Answer: An open curve does not end where it starts, while a closed curve joins back to its starting point.

5. Where do we see a curve in real life?

Answer: We see curves in many places, such as the edges of coins, wheels, rainbows, rivers, and even in handwriting.