Lowest Common Multiple (LCM)

The Lowest Common Multiple (LCM) is an important concept in arithmetic. It defines the smallest multiple of two or more numbers that are in common. Learning LCM is necessary because it helps solve problems involving fractions, ratios, and time intervals. While you're adding fractions with different denominators or finding the exact time two repeating events will tally, LCM is the tool you need.

For example, if you want to find the LCM of 4 and 8, you’re looking for the smallest number that appears in both their lists of multiples, in this case, 8. There are different methods to find the LCM, which include listing out the multiples, using prime factorisation, or using the long division method.

Table of Contents

• What is the Lowest Common Multiple (LCM)?
• Why is LCM Important?
• Methods to Find the LCM
• LCM vs HCF: What's the Difference?
• Examples of Finding the LCM
• Conclusion
• FAQs on Lowest Common Multiple (LCM)

 

What is the Lowest Common Multiple (LCM)?

The Lowest Common Multiple (LCM) is the least number that is a multiple of two or more given numbers. A multiple of a number is the product you get when you multiply the number by any number. For example, the multiples of 2 are 2, 4, 6, 8, and so on.

If you want to find out the LCM of two numbers, which means you’re looking for the least number that is common to both of their multiple lists. Let’s take a look at the multiples of 6 and multiples of 9.

Multiples of 6: 6, 12, 18, 24, 30, and so on.

Multiples of 9: 9, 18, 27, 36, and so on.

The smallest number that occurs in the list of multiples of 6 and 9 is 18, so the LCM of 6 and 9 is 18.

The Lowest Common Multiple is also known as the Least Common Multiple (LCM).

Why is LCM important?

• Equal sharing and grouping: LCM helps when sharing or arranging items into an equal number of groups.

• Process of Scheduling: It is used to find the repeating events that occur at the same time, such as a bus schedule or flight schedules.

• Operations on Fractions: While finding the addition or subtraction of fractions with different denominators, the LCM is used.

• Application in Real-Life Scenarios: To identify the packaging, planning, and organising of the tasks and events that occur in different cycles.

• Core learning for Advanced Maths: Learning LCM creates a foundation for concepts like ratios, number theory and algebra.
  
  

Methods to find the LCM

There are different methods to find the Lowest Common Multiple (LCM) of two or more numbers. Every method identifies the least multiple that is common to all the given numbers. The three frequently used methods are:

1. Listing Multiples

2. Prime Factorisation Method

3. Division (Ladder) Method

This method is preferred depending on the numbers. Let us learn each method step-by-step with examples to understand the concept.

Listing Multiples

The Listing Multiples method is the easy way to find the LCM, which is widely used for small numbers. It is a simple method where LCM is found by listing the multiples of all numbers and choosing the first number that is common to all.

Steps involved in finding the LCM are as follows:

Step 1: List at least 10 multiples of each number.

Step 2: Then identify the least number that is common in the list of all multiples.

Step 3: The least number that is common is the Lowest Common Multiple of the given numbers.

Let us take an example, find the LCM of 2 and 6.

List the multiples of 2 and 6.

• Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, and so on.

• Multiples of 6: 6, 12, 18, 24, 30, and so on.

Common multiples: 12, 24, 30……

LCM = 12

Remember, the listing multiples method is used when the smaller numbers are given, which reminds the multiples of those numbers quickly. And for the large numbers, it is difficult to list the multiples quickly and time-consuming.

Prime Factorisation Method

The Prime Factorisation Method is to list the prime factors of each number and multiply the highest power factors to find the LCM.

Steps involved in finding the LCM are as follows:

Step 1: Write down the prime factors of each number by using repeated division.

Step 2: Write the prime factors in the exponential form.

Step 3: Take the highest exponent and multiply all together.

Step 4: The number obtained is the LCM.

Let us take an example, find the LCM of 24 and 36.

Write the prime factors of 24 and 36.

• Prime factors of 24: 2 × 2 × 2 × 3 = 23 × 3

• Prime factors of 36: 2 × 2 × 3 × 3 = 22 × 32

Now, take the highest powers of all primes:

• 23 (from 24)

• 3² (from 36)

LCM = 23 × 3² = 8 × 9 = 72

To find the LCM for large numbers, this method is more effective. This method involves an understanding of prime numbers, prime factors and exponents.

Division (Ladder) Method

The Division Method is also known as the Ladder Method. This method is used when two or more numbers are given to find the LCM.

Steps involved in finding the LCM are as follows:

Step 1: Arrange the numbers in division or in ladder form.

Step 2: Start dividing the numbers by a common prime number or at least a prime number for one.

Step 3: Here, the prime number will be the factor and the quotient should be written below the number. 

Step 4: Continue dividing until the last row becomes 1.

Step 5: Multiply all the prime numbers to know the LCM of the given numbers.

Let us take an example, find the LCM of 32, 48 and 72.

Multiply all prime numbers: 2 × 2 × 2 × 2 × 2 × 3 × 3 = 288

So, LCM = 288

When more than two numbers are given to find the LCM, this method is preferred. 

LCM vs HCF: What's the Difference?

The table below shows the difference between the LCM and HCF.

 

 

Examples of Finding the LCM

LCM of Two Numbers

Example 1: 

Find the LCM of 10 and 20.

Solution: 

Let’s find the LCM by listing its multiples.

• Multiples of 10: 10, 20, 30, 40, 50, and so on.

• Multiples of 20: 20, 40, 60, 80, and so on.

Common multiples: 20, 40, 60……

LCM = 20

Therefore, the LCM of 10 and 20 is 20.

Example 2:

Find the LCM of 82 and 98 by the prime factorisation method.

Solution:

Write the prime factors of 82 and 98.

• Prime factors of 82: 2 × 41 

• Prime factors of 98: 2 × 7 × 7 = 2 × 72

Now, take the highest powers of all primes:

• 2 and 41 (from 82)

• 7² (from 98)

LCM = 2 × 41 × 7² = 98 × 41 = 4018

Therefore, the LCM of 82 and 98 is 4018.

LCM of Three or More Numbers

Example 3:

Find the LCM of 144, 136 and 224 using the Long division method.

Solution:

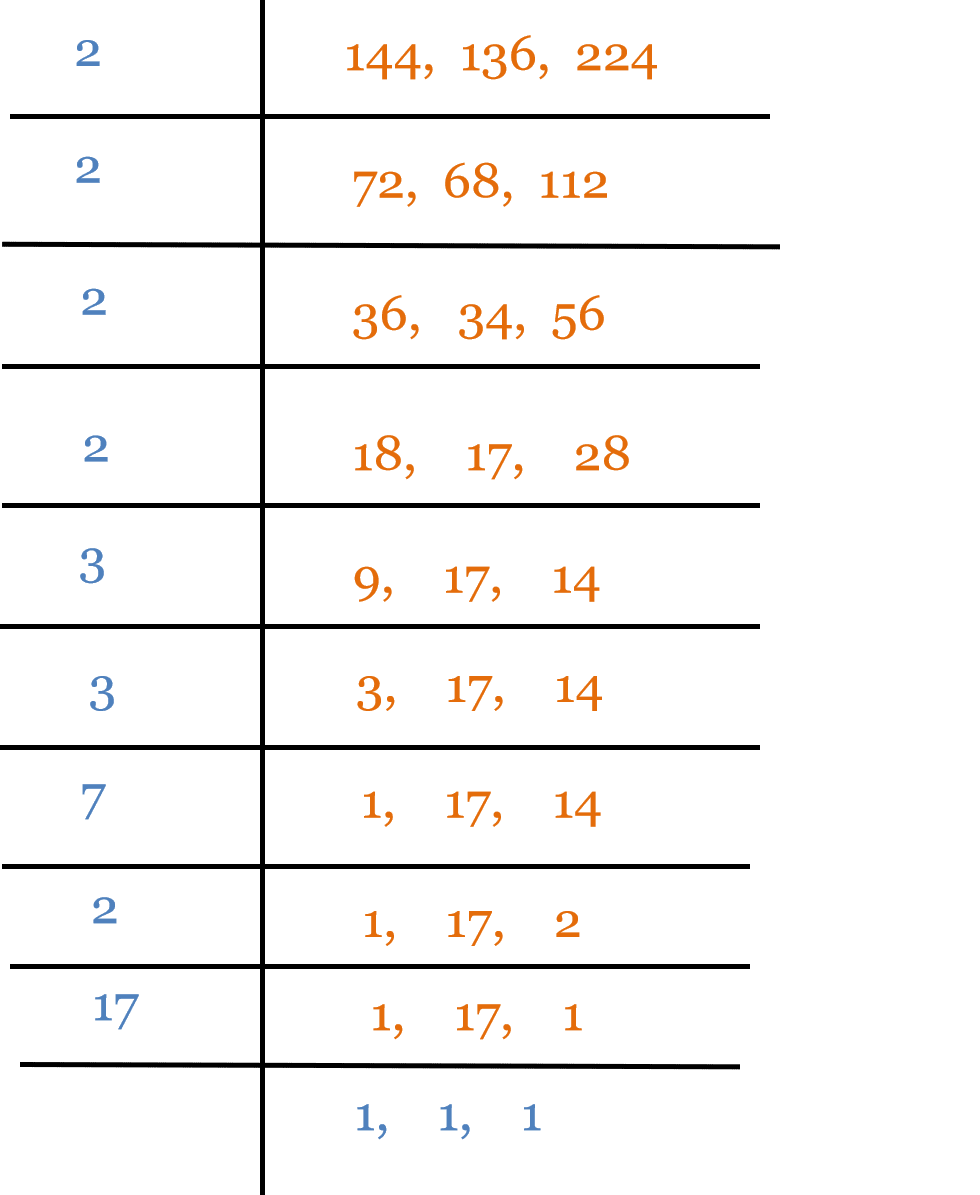
Multiply all prime numbers: 

LCM = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 2 × 17

LCM = 16 × 9 × 14 × 17

LCM = 16 × 9 × 238

LCM = 144 × 238

LCM = 34272

Therefore, the LCM of 144, 136 and 224 is 34,272.

Conclusion

The Lowest Common Multiple (LCM) is a unique concept used to find the least number that is a multiple of two or more numbers. LCM can be found using several ways, like listing multiples, prime factorisation, and the division (ladder) method. 

Bookmark this page and come back whenever you need help on LCM. The more you revise, the quicker you will solve!

Frequently Asked Questions on Lowest Common Multiple (LCM)

Q1: What is the Lowest Common Multiple (LCM)?

Answer: The Lowest Common Multiple or Least Common Multiple is the smallest number that appears in the multiples of two or more numbers.

Q2: What are the different methods used to find LCM?

Answer: The 3 major methods used to find the LCM are: listing multiples, prime factorisation and the division (ladder) method.

Q3: The LCM is bigger than the given numbers. True or False

Answer: True, the LCM is always bigger than the given number or equal to.

Q4: Write the difference between the LCM and HCF. 

Answer: LCM refers to the common multiples and HCF refers to the common factors.

Q5: How to find the LCM of two Co-prime numbers?

Answer: The LCM of two Co-prime numbers is the product of those numbers. Because the co-prime numbers have only 1 as a common multiple. For example, 6 and 7 are co-prime numbers. The LCM is the product of 6 and 7, i.e., 42.