Parallelogram

Introduction to Parallelogram 

A parallelogram in geometry is an important shape that is used in many areas of mathematics. The word comes from the Greek words "parallel" (side by side) and "gramma" (shape). It is a flat, four-sided figure (quadrilateral) where the opposite sides are equal in length and parallel to each other.

Parallelograms have straight sides and are not curved. The opposite angles are always the same, and the angles can be either right angles or slanted. General types of parallelograms include square, rectangle, rhombus, and rhomboid. They are seen in many real-life objects such as tiles, windows, and patterns.

We can find the perimeter of a parallelogram and the area using simple formulas. In this topic, we learn its properties, types, and formulas through step-by-step explanations and solve examples to make understanding easier.

 

Table of Contents

• Definition
• Shape of Parallelogram
• Special types
• Properties
• Real-Life Examples
• Parallelogram vs Rectangle vs Rhombus
• Important Parallelogram Theorems
• Solved Examples
• Conclusion
• FAQs on Parallelogram

 

Definition

A parallelogram is a four-sided shape (quadrilateral) where both pairs of opposite sides are parallel. The opposite sides have the same length, and the opposite angles have the same measure. The same side angle of the cutting line is supplemented with the shape (transversal), which means they add up to 180°. In total, all four angles are always 360°.

If the faces of a three-dimensional object are a parallelogram shape, it is called a parallelepiped. The area of parallelogram depends on the base and the height. The perimeter depends on the length of all four sides.

Shapes such as squares and rectangles have similar properties to a parallelogram. If all four sides of a parallelogram are the same, it becomes a rhombus. If only one pair of opposite sides is parallel and there is no one else, it is called a trapezium.

Example: In a parallelogram ABCD, AB is parallel to CD, and AD is parallel to BC. Also, AB = CD and AD = BC. Angles A and C are the same, and angles B and D are the same. Angle A&D adds up to 180°, and the angle B&C also adds up to 180°.

Quick facts about a parallelogram:

• Number of sides = 4

• Number of vertices: 4

• Parallel sides =  2 pairs

• Area = base × height

• Perimeter = 2 × (the sum of lengths of adjacent sides)

• Type of Polygon = Quadrilateral 

 

Shape of Parallelogram

A parallelogram is a flat, two-dimensional shape with four sides. It has two pairs of sides that are parallel, and the opposite side is equal to the length. If the opposite sides are not equal, the shape cannot be called a parallelogram. In addition, the opposite angles on the inside of a parallelogram should always be equal; if they are not, it is not a parallelogram.

Special types

• Square and Rectangle: The opposite sides of a square and a rectangle are equal and parallel. Their diagonals cut each other into two equal parts.

• Rhombus: A parallelogram where all four sides are equal in length.

  Key Features of a Rhombus:

  • All sides are equal.

  • Opposite angles are equal.

  • Diagonals bisect each other at 90°.

  Rhombus Area Formula: Area = (Diagonal₁ × Diagonal₂) / 2

• Rhomboid: A parallelogram with opposite sides parallel, but the adjacent sides are not parallel with opposite sides. The angles are not right angles.

• Trapezium: A shape with only one pair of parallel sides, while the other two sides are not parallel.

Key Features:

 

Properties

A parallelogram is a basic form of geometry with unique and consistent properties that help solve different mathematical problems. These properties are about the sides, angles, and diagonals, and are used on all types of parallelograms, such as rectangles, rhombuses, and squares. Understanding these characteristics of a parallelogram helps students identify patterns and conditions in the quadrilaterals..

1. The opposite sides are parallel and equal in length

One of the defined properties of a parallelogram is that the opposite sides are equal to length and move in parallel with each other.

Example:

If ABCD is a parallelogram, then:

• AB ∥ CD and AB = CD

• AD ∥ BC and AD = BC

This ensures the shape remains consistent and symmetrical, even when rotated.

2. Opposite Angles are Equal

In a parallelogram, each pair of opposite angles is equal in measure.

Example:

If ∠A and ∠C are opposite angles, then ∠A = ∠C, and ∠B = ∠D.

This property is important for solving angle-based problems in quadrilaterals.

3. Adjacent Angles are Supplementary

Adjacent angles in a parallelogram add up to 180°, meaning they are supplementary.

Example:

• ∠A + ∠B = 180°

• ∠C + ∠D = 180°

This holds true for all corners of the shape and helps in finding missing angles.

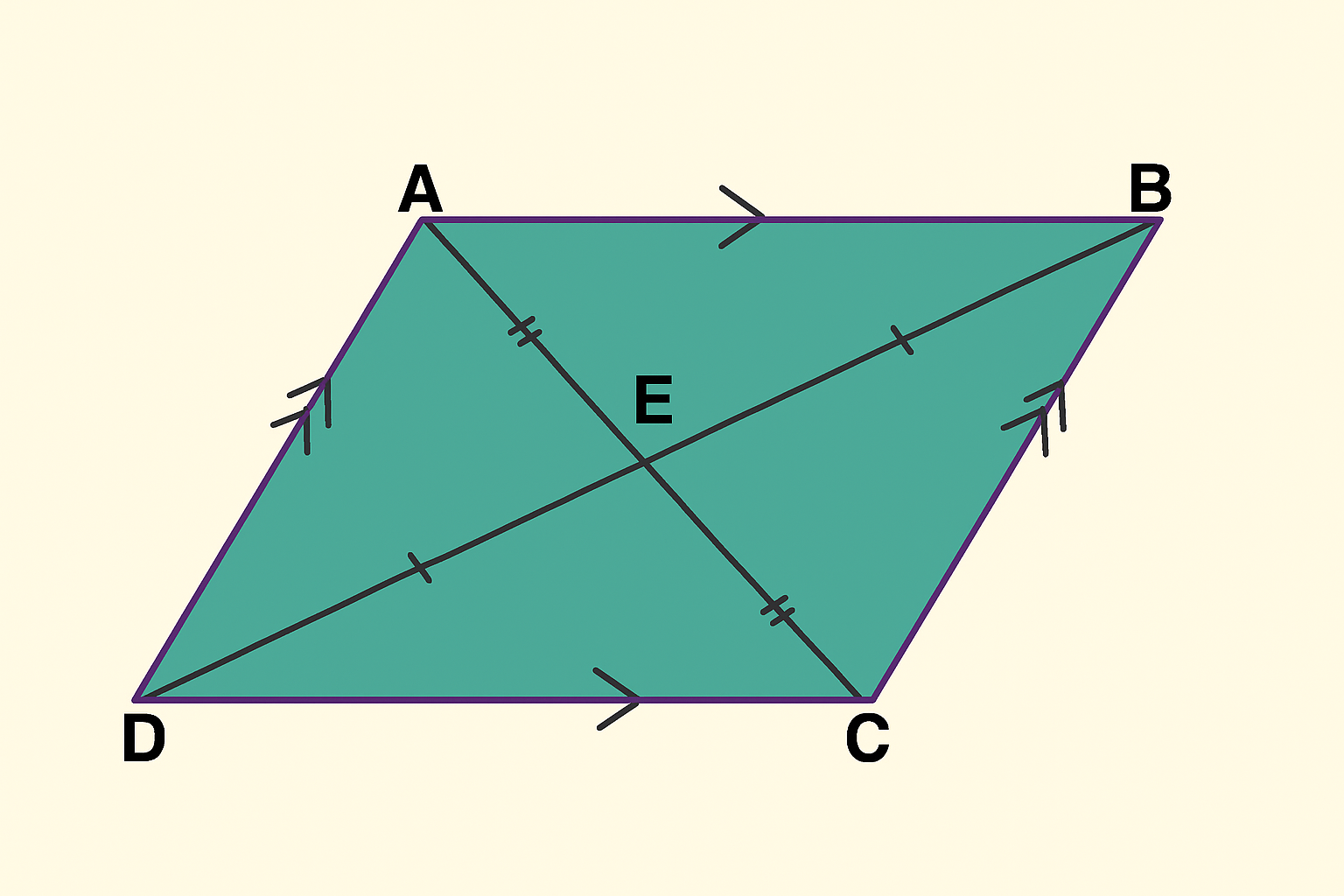
4. Diagonals of a Parallelogram Bisect Each Other

The diagonals of a parallelogram cut each other into two equal parts but are not necessarily equal in length.

Example:

In parallelogram ABCD:

• Diagonal AC and diagonal BD intersect at point E

• Then AE = EC and BE = ED

This property is useful in coordinate geometry and construction-based questions.

5. Sum of Interior Angles

Like all quadrilaterals, the sum of the interior angles of a parallelogram is always 360°.

Example:

• Sum of interior angles = (n − 2) × 180°, where n is the number of sides.

• For a parallelogram (n = 4): (4 − 2) × 180° = 360°.

 

Real-Life Examples

Parallelograms are not only theoretical forms; they appear around us in real structures and objects. Recognizing them helps students connect mathematics to daily life.

Real-Life Parallelogram Examples Table:

Parallelogram vs Rectangle vs Rhombus

This comparison helps differentiate the subtypes of parallelograms based on their specific geometric properties.

Comparative Table:

 

Important Parallelogram Theorems

Parallelograms play an important role in the theorem geometry and help understand the deep properties of the shapes. These parallelogram theorems are particularly useful for solving evidence, construction, and coordinate geometry problems. Let's find the two important theories commonly used in mathematics in secondary school and high school.

Parallelograms on the Same Base and Between Same Parallels

This is one of the most fundamental theorems in geometry.

• Theorem: Parallelograms on the same base and between the same pair of parallel lines are equal in area.

• Explanation: If two or more parallelograms share the same base and lie between the same parallel lines, they will have equal area regardless of their shape or slant.

• Diagram Concept: Two parallelograms ABCD and ABEF, on the same base AB and between the same parallels AB and CF.
  Then, Area(ABCD) = Area(ABEF)

Key Points:

• The base must be common.

• Both shapes must lie between the same parallel lines.

• This theorem helps in proving area-based problems.

Diagonals and Angle Theorems

The diagonal & angle theorems in parallelograms explain the behavior of internal measurements.

Diagonal Theorem:

• In a parallelogram, the diagonals bisect each other.

• That means each diagonal cuts the other into two equal parts.

Example: If diagonals AC and BD intersect at point E, then:

• AE = EC

• BE = ED

Angle Theorems: Some useful angle theorems in parallelograms include:

• Opposite angles are equal

• Adjacent angles are supplementary (i.e., add up to 180°)

• If one angle is a right angle, all angles are right angles (used in proving rectangles)

Solved Examples

Understanding parallelograms through solved examples helps to strengthen concepts such as fields, circumference, properties, and applications in real life. This section provides a mix of basic numerical examples, proof-based geometry questions, and problems in the real world that show how to effectively use parallelogram formulas and theorems.

Basic Examples with Area and Perimeter

These examples involve the direct application of formulas for the area of a parallelogram and the perimeter of a parallelogram.

Formula Recap:

• Area = base × height

• Perimeter = 2 × (length + breadth)
  

Example 1: Find the area of a parallelogram with base = 8 cm and height = 5 cm.

Solution: Area = 8 × 5 = 40 cm²

Example 2: A parallelogram has sides 6 cm and 4 cm. Find its perimeter.

Solution: Perimeter = 2 × (6 + 4) = 20 cm

Example 3: Prove that the diagonals of a parallelogram bisect each other.
Solution:

• Given: Parallelogram ABCD, diagonals AC and BD intersect at E.

• To Prove: AE = EC and BE = ED

• Proof:
  △ABE ≅ △CDE (by SAS congruence)
  ⇒ AE = EC and BE = ED
  Hence, the diagonals bisect each other.

Example 4: A garden is in the shape of a parallelogram with a base of 10 m and height of 7 m. What is the area of the garden?
Solution: Area = base × height = 10 × 7 = 70 m²

Example 5: A designer uses parallelogram tiles that are 12 cm long and 8 cm wide. What is the perimeter of each tile?
Solution: Perimeter = 2 × (12 + 8) = 40 cm

 

Summary Table: Solved Parallelogram Examples

Visual Aids and Diagrams

Visual representation is important for understanding the term of parallelograms. Diagrams help students identify the side length, the angle, and different elements of a parallelogram. This section focuses on labeled diagrams and interactive grid examples to imagine & strengthen the concept of different types of parallelograms.

Labelled Diagrams of Each Parallelogram Type

Understanding the variations among parallelograms is easier when each type is illustrated with clearly labelled diagrams.

Commonly Labeled Elements:

• Opposite sides (marked equal)

• Angles (opposite angles are equal)

• Diagonals (showing bisection)

• Right angles (in rectangles/squares)

• Side lengths (indicated with units)

Diagrams:

Conclusion

Parallelogram geometry has basic forms that help create a strong understanding of angles, side properties, and field calculations. From architectural designs to engineering and everyday patterns, parallelograms and their special form, the rectangle,  rhombus, and square, are countless applications in the real world. By mastering the properties, theorems, and formulas associated with Parallelograms, students can solve a wide range of geometric problems with confidence and accuracy.

 

FAQs on Parallelogram

1. What are the 4 types of parallelograms?

Ans: The four main types of parallelograms are rectangles, rhombuses, squares, and rhomboids (sometimes called rhomboids). 

• Rectangle: A parallelogram with four right angles.

• Rhombus: A parallelogram with all four sides of equal length.

• Square: A parallelogram with four right angles and all four sides of equal length.

• Rhomboid: A parallelogram where opposite sides are parallel, but adjacent sides are of unequal lengths, and the angles are not right angles.

2. What are the 7 properties of a parallelogram?

Ans: 

• The opposite sides are parallel and equal

• The opposite angles are equal

• The consecutive or adjacent angles are supplementary

• If any one of the angles is a right angle, then all the other angles will be at a right angle

• The two diagonals bisect each other

• Each diagonal bisects the parallelogram into two congruent triangles

• The Sum of the squares of all the sides of a parallelogram is equal to the sum of the squares of its diagonals. It is also called the parallelogram law

3. Is a kite a parallelogram?

Ans: No, a kite is not a parallelogram. A parallelogram is defined as a quadrilateral with two pairs of parallel sides, while a kite has two pairs of adjacent sides of equal length & does not have any parallel sides.

4. How do you measure a parallelogram?

Ans: The formula to find the area of a parallelogram is: Area = b*h. With the parallelogram sitting flat, the b stands for the base, or the side that is flat on the ground & the h stands for height, or the distance between the bottom and top sides.

5. Is a diamond a parallelogram?

Ans: A diamond is a two-dimensional flat quadrilateral with four closed straight sides. A diamond is also called a rhombus because its sides are of equal measure and because the opposite angles are equal. Diamonds are also considered to be parallelograms because their opposite sides are parallel to each other.