Pythagoras Theorem

Introduction

The Pythagoras theorem is one of the most important topic in mathematics and geometry. It is also known as the Pythagorean Theorem and is a fundamental concept. This theorem explains the relationship between the sides of a right-angled triangle. The name originated after the ancient Greek mathematician Pythagoras, who claimed to have proved the theorem. The theorem is not only applicable in mathematics, but it also has broad applications in construction, computer graphics, navigation and science. Let us explore Pythagoras theorem, its formula, and derivation with solved examples. In this article, we'll go through the definition of the Pythagorean theorem, its formula, practical applications and sample example. This page will help you in easily understanding and applying the formula for the Pythagorean theorem.

 

Table of Contents

• What is the Pythagorean Theorem?
• Pythagorean Theorem Formula
• History of the Pythagorean Theorem
• Understanding the Pythagoras Property
• How to Use the Pythagorean Theorem
• Applications of the Pythagorean Theorem in Real Life
• Derivations and Proofs
• Pythagorean Triples
• Advanced Concepts: Coordinate Geometry
• Solved Examples
• Practice Questions
• Conclusion
• FAQs on Pythagoras Theorem

 

What is the Pythagorean Theorem?

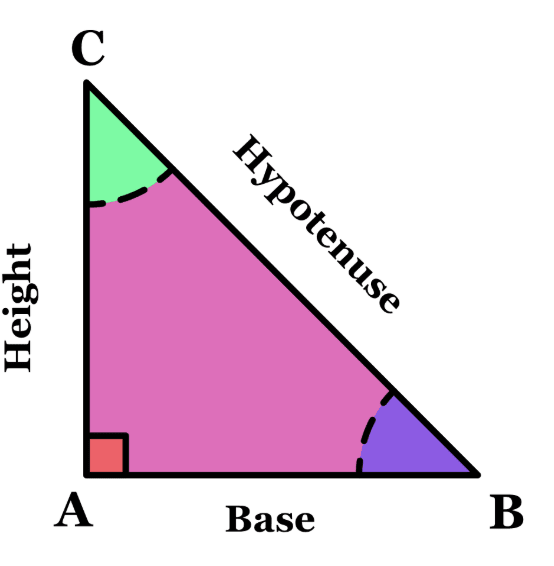
The Pythagorean Theorem, sometimes referred to as the Pythagoras Theorem, states that in any triangle with a 90 degree angle (a right angled triangle), the square of the longest side (called the hypotenuse) is equal to the sum of the squares of the other two sides. In other words, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Along with mathematics, we apply this theorem widely in construction, navigation, and computer graphics.

For example, for the triangle ABC, AB is the base, AC is the height and BC is the hypotenuse. Thus, BC² = AB² + AC²

 

Pythagoras Theorem Formula

The Pythagorean theorem is expressed using the formula as shown below:

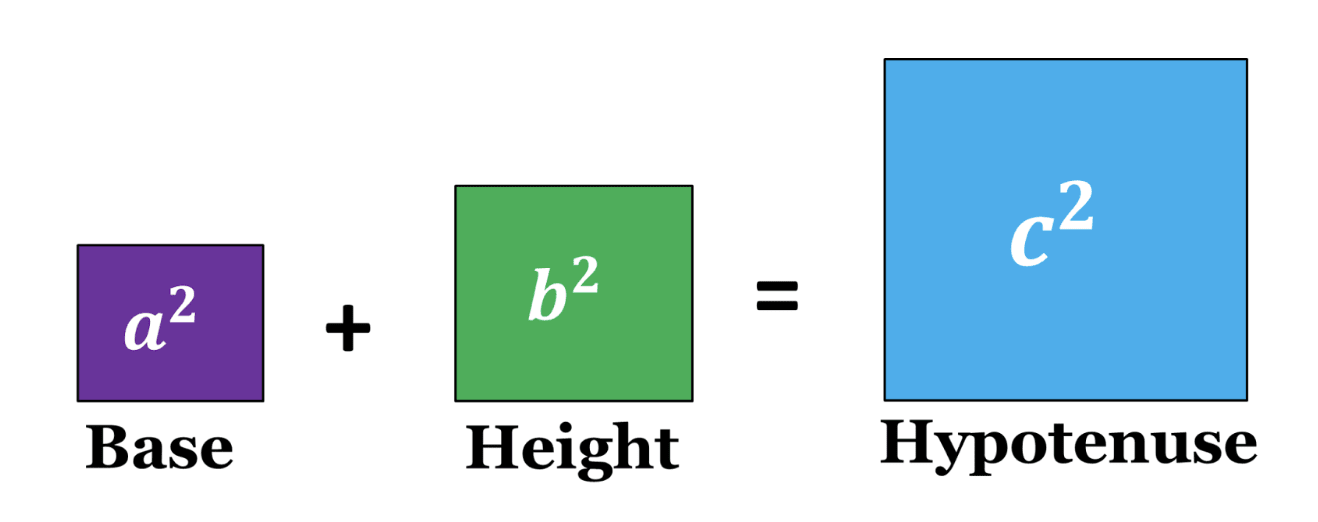
Hypotenuse² = Perpendicular² + Base² 

For a right triangle ABC with sides a,b and c the Pythagoras Theorem Formula will be c² = a² + b²

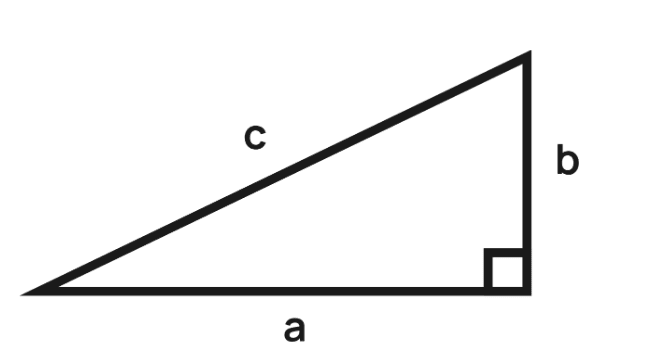
Where:

• c is the hypotenuse (longest side),

• a and b are the other two sides.

This rule is called the Pythagoras property, and it only works for right angled triangles. It’s one of the first and most useful geometric rules students learn, especially because it shows up often in daily life.

Understanding the Terms:

• Right-angled Triangle: The triangle where one of the angles is exactly 90.
• Hypotenuse: The longest side of a right-angled triangle.
• Legs: The other two sides, i.e., base and height of a right-angled triangle.

 

History of the Pythagorean Theorem

This theorem is named after a Greek mathematician and philosopher Pythagoras who lived around 500 BCE. Although, the concept was known even before his time Pythagoras was the first to provide a fixed proof of the theorem, Records from Babylon and India show existance of this rule before thousands of years. Over centuries, this idea has become a key part of math education across the world.

 

Understanding the Pythagoras Property

Let’s imagine a triangle with a 90 degree angle. If you draw squares on each of its three sides, the area of the biggest square (on the hypotenuse) is exactly equal to the combined area of the other two squares. This visual representation helps us see the pythagoras property in action. 

So by Pythagoras Theorem Formula - Area of square “a” + Area of square “b” = Area of square “c”

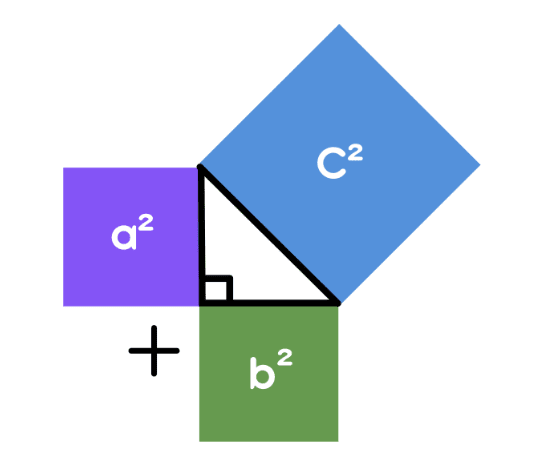
This relationship gives us a reliable way to calculate missing sides in right angled triangles, even without measuring them physically. This means that if you know any two sides of a right angled triangle, you can find the third.

Example:

If a = 6 and b = 8, what is c?

c² = 6² + 8² = 36 + 64 = 100 → c = $\sqrt{100}$ = 10

So, the hypotenuse is 10 units long.

This pythagoras formula is used not just in school problems, but also in fields like engineering, physics, navigation, and more.

 

How to Use the Pythagorean Theorem

Here’s how you can solve real problems using the pythagorean theorem formula:

Finding the Hypotenuse:

If you know the two shorter sides, use c² = a² + b²

Finding a Side:

If you know the hypotenuse and one side, use:
a² = c²   b²

Real Life Word Problem:

A ladder leans against a wall. The ladder is 13 ft long, and it touches the wall 5 ft above the ground. How far is the base of the ladder from the wall?

Use c = 13, a = 5

b² = 13²   5² = 169   25 = 144 → b = √144 = 12

The base is 12 ft from the wall.

 

Applications of the Pythagorean Theorem in Real Life

The pythagorean theorem is incredibly useful and practical in real world situations:

Architecture & Construction

Builders use the pythagoras formula to check if angles are right, ensuring walls and supports are straight and stable.

Navigation & Mapping

When finding the shortest distance between two points (like a plane flying diagonally), navigators use the pythagorean theorem formula.

Sports & Athletics

In soccer or basketball, coaches and players use it to calculate angles and distances between players.

Robotics & Engineering

Engineers use the pythagoras property to design robots, buildings, or even highways with precise measurements.

Computer Graphics & Gaming

The pythagoras theorem helps calculate distance between objects or characters on the screen.

 

Derivations and Proofs

There are over 300 known proofs of the pythagoras theorem! Here are two popular ones:

A. Geometric Proof

1. Draw a square with side (a + b).

2. Place 4 identical right triangles inside.

3. The empty space forms a square of side c.

4. Use area formulas to derive: c² = a² + b²
   
   

B. Algebraic Rearrangement

Using algebra, rearrange squares and triangles to visually show that the formula must be true.

These proofs make the pythagoras formula not just useful, but also fascinating to study.

 

Pythagorean Triples

Some right angled triangles have sides with whole numbers. These sets of numbers are called Pythagorean Triples. In other words, Pythagorean Triples are special sets of three whole numbers that follow the Pythagoras Theorem.

Examples:

• 3, 4, 5

• 5, 12, 13

• 7, 24, 25

These are helpful for solving problems quickly without a calculator and reinforce the understanding of the pythagoras theorem.

 

Advanced Concepts: Coordinate Geometry

In coordinate geometry, we use the pythagorean theorem formula to find distance between two points.

Distance Formula:

Distance = √[(x₂   x₁)² + (y₂   y₁)²]

This is directly derived from c² = a² + b², with horizontal and vertical distances forming a right triangle on the graph.

Solved Examples on Pythagoras Theorem

Example 1: Find the base of a right-angled triangle, where the height is 12 cm and the hypotenuse length is 13 cm.

Solution:

Given,

Height = 12 cm

Hypotenuse = 13 cm

Base =?

We know that,

Pythagoras Formula: 

Hypotenuse² = Base² + Height²

13² = Base² + 12²

Base² = 13² - 12²

Base² = 169 - 144

Base²=25

Base=$\sqrt{25}$

Base = 5 cm

Therefore, the base of a right-angled triangle is 5 cm.

 

Example 2: 8, 15 and 17 units are sides of a triangle. Prove that the triangle is right-angled.

Solution:

We know that,

Pythagoras Formula: 

Hypotenuse² = Base² + Height²

Base = 8 units

Height = 15 units

Hypotenuse = 17 units [Because the longest side is the hypotenuse side]

Hypotenuse² = Base² + Height²

17² =8² + 15²

289 = 64 + 225

289 = 289

LHS = RHS

Hence, proved that the given triangle is right-angled.

 

Example 3: The side of a square is 9 cm. Find the length of the diagonal of a square.

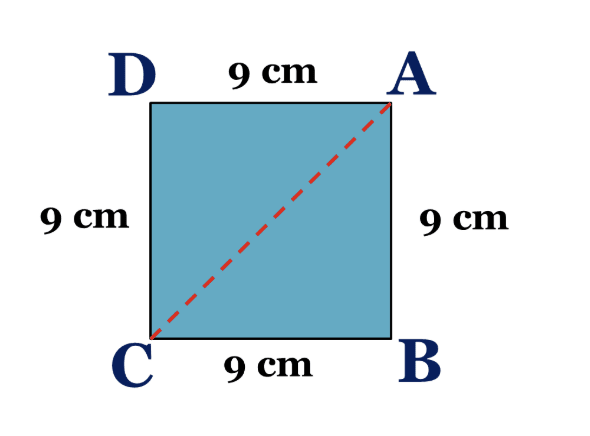
Solution:

Given,

Side = 9 cm

Diagonal =?

Let's consider two right-angled triangles, i.e., ADC and ABC.

ADC = ABC

Apply Pythagoras theorem,

In ADC,

AC²=AD² + DC²

AC² = 9² + 9²

AC² = 81+ 81

AC² = 162

AC = $\sqrt{162}$

AC = $\sqrt{81}$ x $\sqrt{2}$

AC=9$\sqrt{2}$ cm

Therefore, the length of a diagonal is 92 cm.

 

Example 4: A sailor sails a ship 12km east and 15km north. Find the distance from the starting point.`

Solution:

Let’s consider BAC

We know that,

Pythagoras Formula: 

Hypotenuse² = Base² + Height²

BC² = AC² + AB²

BC² =12² + 15²

BC² = 144+225

BC² = 369

BC = $\sqrt{369}$

BC = 3$\sqrt{41}$ km

Therefore, the distance from the starting point is 3$\sqrt{41}$ km

 

Practice Questions

1. A right-angled triangle has legs of length 7 cm and 24 cm. Find the length of the hypotenuse.

2. A right-angled triangle has a hypotenuse of length 17 inches and one leg of length 8 inches. Find the length of the other leg.

3. A rectangular garden is 12 meters long and 5 meters wide. What is the length of the diagonal of the garden?

4. A baseball diamond is a square with sides of 90 feet. What is the distance from home plate to second base?

 

Conclusion

The Pythagoras Theorem is a timeless rule that shows the relationship between the sides of a right triangle. From the simple pythagoras formula to its wide use in daily life, the pythagoras property remains a key concept in both education and professional fields. With Pythagorean theorem formula, you can solve countless geometry problems and real world challenges. Whether you're a student or someone who loves math, understanding this theorem gives you a solid base to explore more advanced topics.

 

Frequently Asked Questions on Pythagoras Theorem

1. What is the full Pythagoras formula?

Answer: The full Pythagoras formula is c² = a² + b², where:

• c is the hypotenuse (the longest side),

• a and b are the other two sides of a right-angled triangle.
  This formula helps calculate the length of any one side when the other two are known.

 

2. What is the Pythagorean theorem explain?

Answer: The Pythagorean Theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In formula form:

c² = a² + b²

This theorem is used to find distances, heights, and side lengths in geometry and real life applications.

 

3. How to calculate angle in Pythagoras theorem?

Answer: While the Pythagorean Theorem itself doesn’t give angles, you can find angles using trigonometry with the sides:

• sin(θ) = opposite / hypotenuse

• cos(θ) = adjacent / hypotenuse

• tan(θ) = opposite / adjacent
  Then, use a calculator’s inverse functions (like sin⁻¹, cos⁻¹) to get the angle in degrees.

 

4. How to calculate triangle area?

Answer: The area of a triangle is calculated using the formula:

Area = ½ × base × height

For a right triangle, the base and height are usually the two sides that form the right angle.

 

5. Is a² + b² = c² only for right triangles?

Answer: Yes, the formula a² + b² = c² is only valid for right-angled triangles. If the triangle does not have a 90° angle, this rule doesn’t apply. For non-right triangles, use the Law of Cosines instead.

 

Unlock the power of the Pythagorean Theorem and more with simple, engaging math lessons at Orchids The International School.