Divide

The divide in maths means to perform division. The division is used for equal sharing and equal grouping. It is one of the basic arithmetic operations among the four operations. In other words, division is dividing a group of large items into smaller groups with an equal number of items in each. The Sanskrit term for divide is “Bhāga / Bhāgaharaṇa”. Let us understand the division concept, symbol of division, formula, properties of division and solved examples.

Table of Contents

• What is Divide?
• Division Symbol
• Parts of the Division
• Division Facts
• How to Divide the Numbers?
• Long Division Method without Remainder
• Long Division Method with Remainder
• Examples of Dividing Numbers
• Conclusion
• FAQs on Divide

What is Divide?

The divide says to perform a division operation. The division is nothing but repetitivesubtraction.It is also the inverse of multiplication. This arithmetic operation breaks large numbers into smaller groups where each group contains an equal number of items. Suppose, for a cultural event in school, a teacher should divide students into equal groups, then the division is used. Assume there are 120 students in a school, and the teacher should divide them into 10 equal groups. Then, divide 120 by 10. The result is 12. Therefore, there will be 10 groups with 12 students in each group.

Division Symbol

The general division symbol in mathematics is represented by a small straight line with dots above and below the line (÷). It is also expressed by a small slanting line or slash. Let's see some examples: 24 ÷ 2 is the same as 24/2. 24 ÷ 2 = 12 and 24/2 = 12.

Parts of Division

The terms used in the division process are the parts of division. There are four parts or terms, i.e., divisor, dividend, quotient, and remainder. Let us observe the table below for a better understanding of the terms with an example. 

Example: Divide 123 by 2. When we divide 123 by 2, the result will be 61 is the quotient, and 1 is the remainder.

 

 

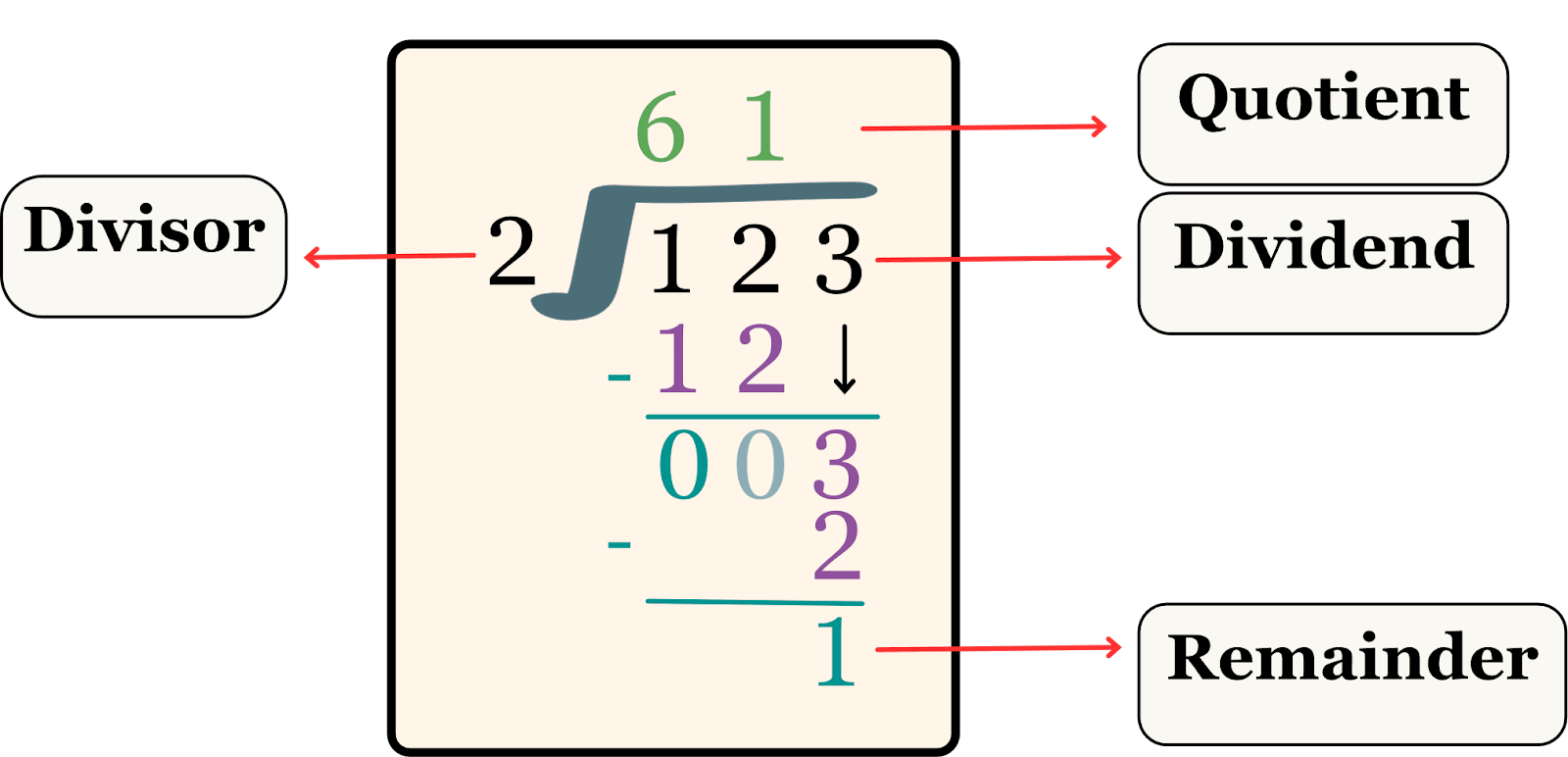
The above image shows the parts of the division that are the divisor, dividend, quotient, and remainder. 

Division Facts

The division fact says that the product of the divisor and quotient, added to the remainder, is always equal to the dividend. 

This formula is also known as the division algorithm. The formula is widely used to verify the division. Substitute the values of divisor, dividend, quotient and remainder into the formula and check the result. 

Example: Divide 18 by 4. When we divide 18 by 4, we get a quotient of 4 and a remainder of 2.

How to divide the numbers?

Dividing the numbers involves the process of separating a number, basically called the dividend, into equal parts with the help of another number called the divisor. After dividing, the result obtained is called the quotient and if any leftover, it is called the remainder.

The two major types of division are:

1. Division without remainder

2. Division with remainder

Let us understand both with the help of examples.

Long Division Method Without Remainder

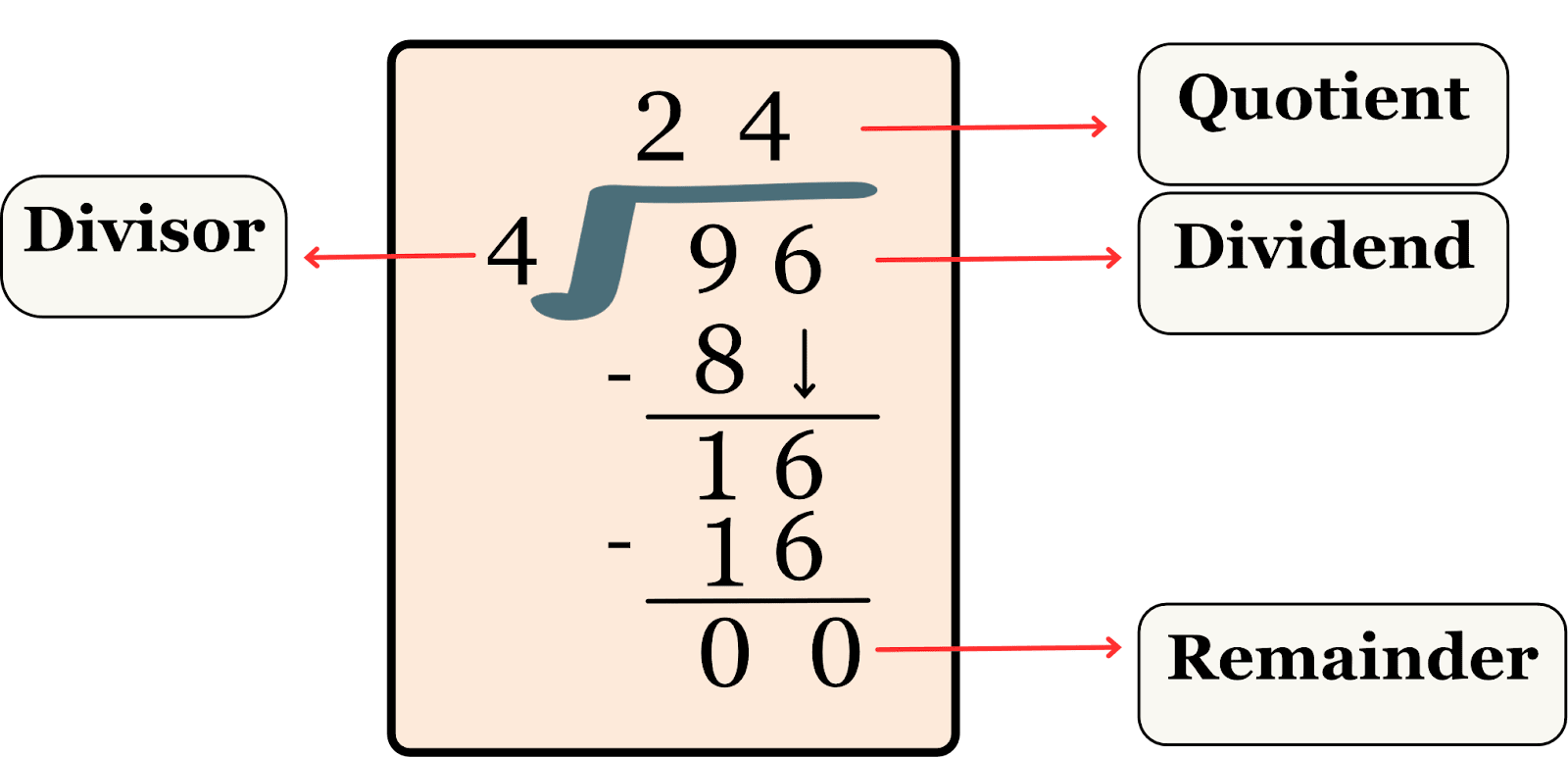
Let us take the example of 96 divided by 4.

Step 1: Arrange the divisor (4) on the left side of the symbol ⟌ and the dividend (96) on the right side of the symbol.

Step 2: Check the first digit of the dividend from left, i.e., 9, which is less than the divisor 4. Thus, we can divide easily. If the digit is greater than the divisor, then take the first two digits of the dividend.

Step 3: Now divide the selected digit 9 by the divisor 4. 9 ÷ 4 = 2, write 2 above as a quotient. That is because 4 × 2 = 8.

Step 4: Subtract 8 from 9. 9 - 8 = 1. Write 1 below.

Step 5: Bring down the next digit of the dividend, i.e., 6. So, the number becomes 16.

Step 6: Now we should divide 16 by 4. We know that 4 × 4 = 16.

16 ÷ 4 = 4

Write 4 above as a quotient.

Step 7: Subtract 16 from 16. The result is 0. The remainder is 0, which says division is done.

Therefore, 96 ÷ 8 = 12

Long Division Method With Remainder

Dividing numbers with remainder is nothing but after division, there will be a leftover number that cannot be divided by the divisor. 

Let us take the example of 89 divided by 2.

Step 1: Arrange the divisor (2) on the left side of the symbol ⟌ and the dividend (89) on the right side of the symbol.

Step 2: Check the first digit of the dividend from left, i.e., 8, which is less than the divisor 2. Thus, we can divide easily. If the digit is greater than the divisor, then take the first two digits of the dividend.

Step 3: Now divide the selected digit 8 by the divisor 2. 8 ÷ 2 = 4, write 4 above as a quotient. That is because 2 × 4 = 8.

Step 4: Subtract 8 from 8. 8 - 8 = 0. Write 0 below.

Step 5: Bring down the next digit of the dividend, i.e., 9. So, the number becomes 9.

Step 6: Now we should divide 9 by 2. We know that 2 × 4 = 8.

9 ÷ 2 = 4

Write 4 above as a quotient.

Step 7: Subtract 8 from 9. The result is 1. The remainder is 1, which is less than the divisor 2. So, further cannot be divided, leaving a remainder.

Therefore, 89 ÷ 2 = 44 quotient and 1 remainder.

Examples of Dividing Numbers

Example 1: There are 300 flowers and the vendor should prepare 30 bouquets. Find out how many flowers vendors will include in each bouquet.

Solution: 

Given,

There are 300 flowers.

30 bouquets need to be prepared.

To find the number of flowers in each bouquet.

So, divide 300 ÷ 30.

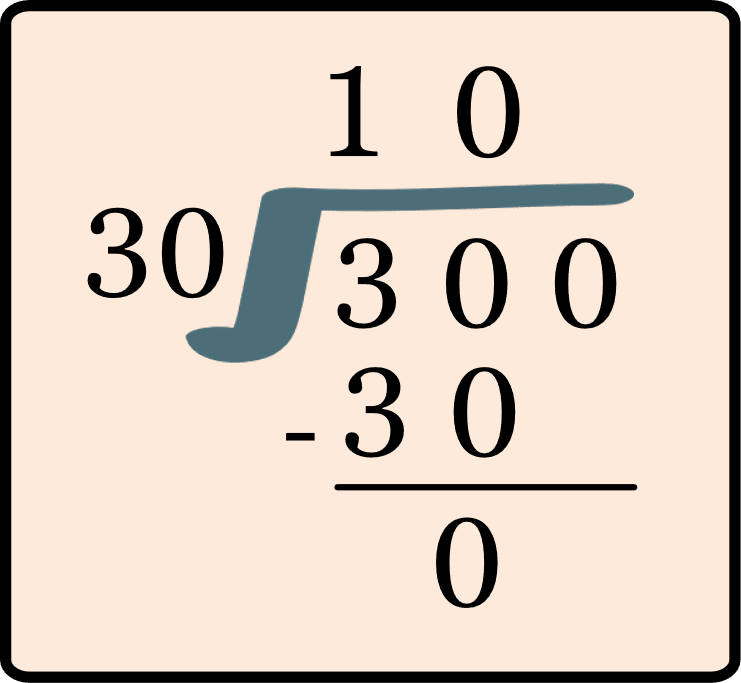
Therefore, 10 flowers are required in each bouquet.

Example 2: Divide 455 ÷ 10

Solution: 

When dividing any number by 10, the ones digit will be the remainder and the remaining digits will be the quotient. 

Thus, 455 ÷ 10 = 45 Q and 5 R

Example 3: Divide and verify the result. 80 ÷ 4

Solution:

First, divide 80 by 4.

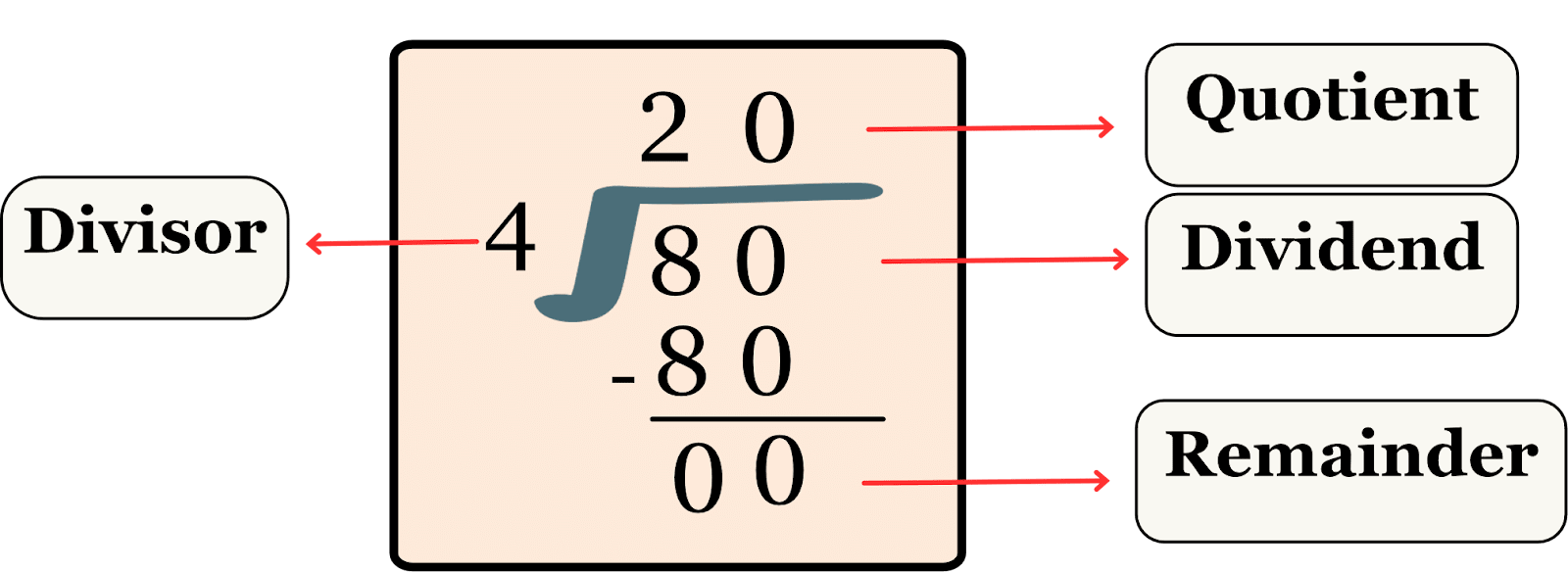
To verify the result use Dividend = (Divisor × Quotient) + Remainder

80 = (4 × 20) + 0

80 = (80) + 0

80 = 80

Hence, verified.

Example 4: Divide 121 by 11.

Solution: 

We have to divide 121 by 11. 121 is the dividend and the divisor is 11.

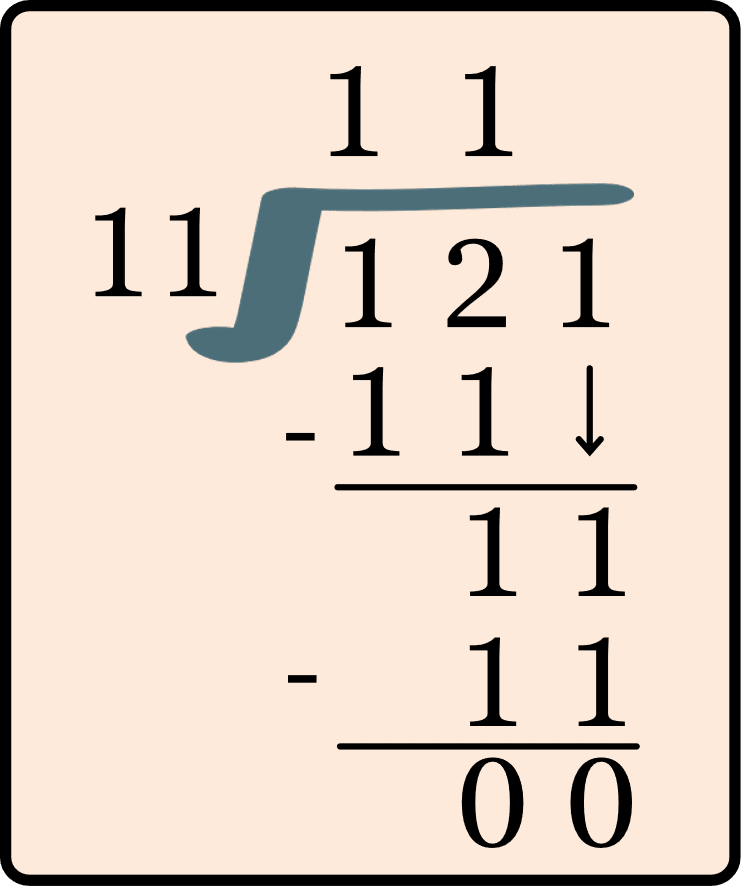
Therefore, the quotient is 11 and the remainder is 0.

Conclusion

Dividing the numbers means splitting the large numbers into smaller ones. It's necessary to understand the terms dividend, divisor, quotient, and remainder while doing division. The result of dividing numbers may be whole numbers, fractions or even decimals. Don’t get confused between divide and division, both are the same. When you get confused, come back to this page and learn the concept to avoid confusion. 

FAQs on Divide

Q1: Is divide and division the same?

Answer: Yes, both divide and division are the same. The dividing process is known as division.

Q2: What are the parts of the division?

Answer: There are four parts to division. They are dividend, divisor, quotient and remainder.

Q3: How do you divide when the Divisor is bigger than the Dividend?

Answer: If the divisor is bigger than the dividend, that means you are dividing a small number by a large number. One way is to add zero to the right of the dividend until the number is suitable for dividing and the result will be in a fraction or decimal.

Q4: Divide 100 by 10.

Answer: To divide any number by 10, move the ones digit of a number after the decimal point. 100 ÷ 10 = 10.

Q5: 1 can be divided by any positive number. True or False

Answer: False, 1 cannot be divided by any positive number because the result leads to a real number between 0 to 1.