Prism

Introduction to Prism

A prism is a three-dimensional shape that contains two identical faces called bases and other faces that are rectangles that join the bases. The word "prism" comes from the Greek word “prisma”, which means something that is cut or sawed, because a prism looks like a cut ​​piece of a solid shape.

Prisms may be based on different shapes, such as triangles, rectangles, or pentagons. It gives us a triangular prism, a rectangular prism, a pentagonal prism, and more. Prisms have faces, edges, and vertices, and we can calculate their volume, surface area, and perimeter using simple formulas. Common examples in real life are boxes, Toblerone chocolates, tents, and water tanks.

In this article, we will learn about the types of prisms, their properties, and formulas. Step-by-step examples will make it easier to understand how to identify a prism and solve problems related to them in daily life.

Table of Contents  

• Prism Shape
• Cross Section of Prism
• Types of Prism
• Right Prism and Oblique Prism
• Formulas
• Surface Area of a Prism
• Volume of a Prism
• Properties of a Prism
• Applications of Prism in Real Life
• Solved Examples
• FAQs on Prism

 

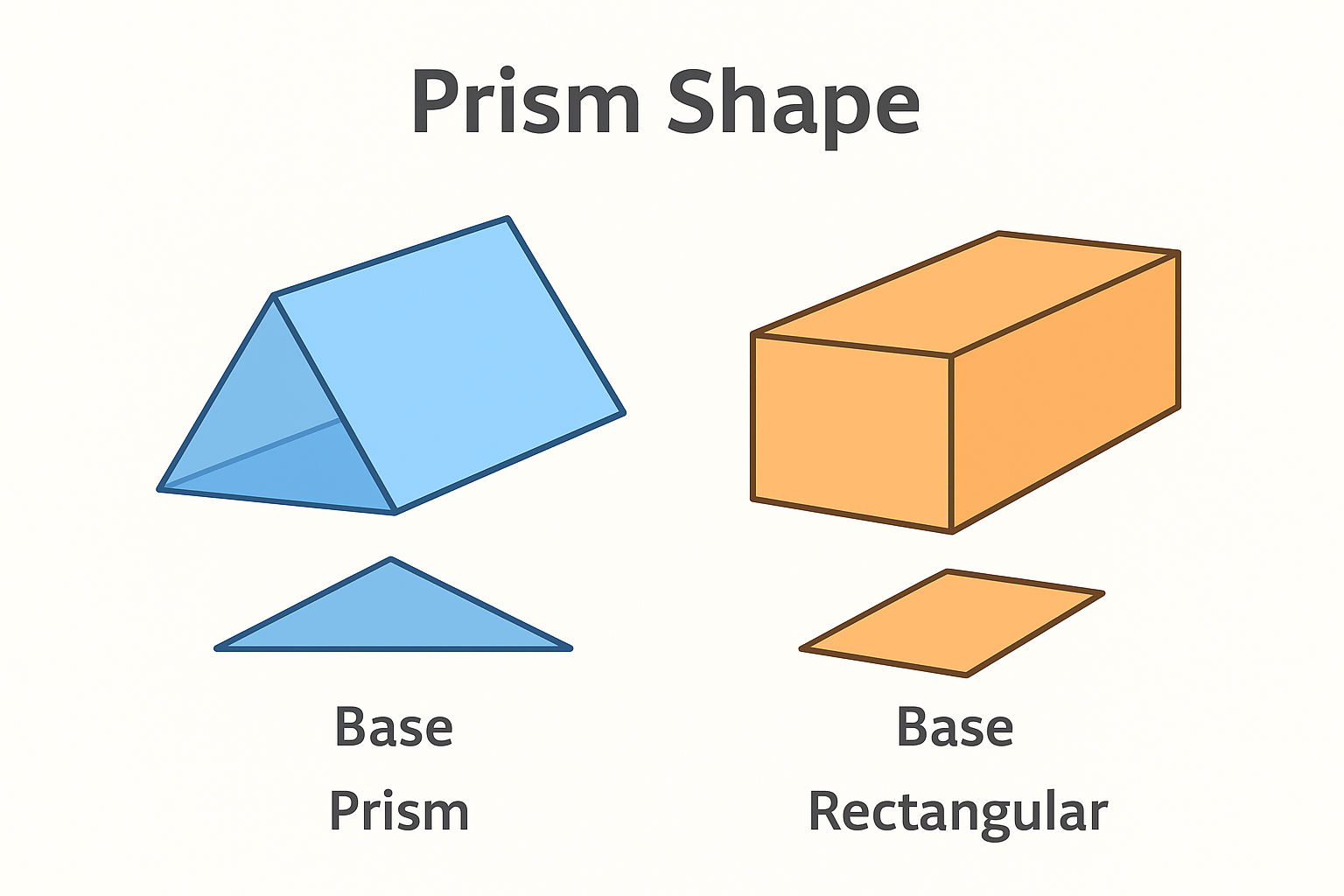
Prism Shape

A prism is a solid three-dimensional shape with two identical ends called the bases, flat faces, and the same cross-section in its length. The base can be a shape such as a triangle, square, rectangle, or other polygon, but not a circle. For example, if the base is a triangle, the prism is called a triangular prism. All faces on a prism are flat, and the shape does not have any curves.

Cross Section of Prism

The cross-section of a prism is the shape we get when we cut a prism with a plane along the length. The cross-section is always the same as the shape of the base. For example, if we cut a square prism parallel to the base, the cross-section will also be a square. Similarly, a triangular prism cut in parallel to the base will have a triangular cross-section.

Types of Prism

A prism is a 3D figure that has the same shape on top and bottom, called the bases. Depending on how these bases look, a prism is divided into two main types: a regular prism and an irregular prism.

• Regular prism: If the basis of the prism is a regular polygon (all sides and angles are equal), it is called a regular prism. For example, a prism is a regular prism with bases in the shape of a square or equilibrium triangle.

• Irregular prism: If the base is made of an irregular polygon (sides and angles are not equal), it is called an irregular prism. For example, if the base looks like an uneven shape, the prism becomes irregular.

Prisms Based on the Shape of the Bases

Apart from regular and irregular, a prism is also named after the shape of its bases. Here are some common types:

• The triangular prism has two triangular bases.

• A square prism has two square bases.

• A rectangular prism has two rectangular bases.

• The pentagonal prism has two pentagon-shaped bases.

• The hexagonal prism has two hexagon-shaped bases.
  
  

Right Prism and Oblique Prism

A prism is a solid shape that contains two equal and parallel bases, and the sides connect these bases. Prisms can be of many types, and one way to divide them is into the right prism and the oblique prism. The main difference between them is how since faces are in relation to the base.

In a right prism, the side faces stand straight on the base, so the prism looks "straight up". But in an oblique prism, the sides are slanted and not at 90° to the base. From this, the prism seems to bend to one side. Although their shapes look different, both prisms have the same formula for the surface and volume.

Here is a simple table to understand the difference:

 

Formulas

A prism is a 3D shape. Since it has length, width, and height, it has surface area and volume. Let's easily learn both.

• Surface Area of a Prism 

• Volume of a Prism

Surface Area of a Prism

The surface area means the total area of all the faces of the prism. The formula is:

 Surface Area = 2 × (Base Area) + (Base perimeter × Height)

This means:

• Take 2 base faces (like top and bottom)

• Add the sides (around the shape)

Volume of a Prism

The volume means how much space the prism takes inside. The formula is : 

Volume of Square Prism = Base Area × Height

V =  s² × h cubic units

Here,

• s = side of the square

• H = height of the prism

• So, volume tells us how many “blocks” can fit inside the prism.
  
  

Properties of a Prism

 A prism has two identical bases.

•  The sides (lateral faces) are parallelograms.

•  It has a uniform cross-section along its height.

•  The number of faces, edges, and vertices depends on the base polygon. 
  
  

Applications of Prism in Real Life

•  Optics: Glass prisms split white light into different colours.

•  Architecture: Many buildings use rectangular prism shapes.

•  Engineering: Bridges and supports often utilise prism structures for stability.

•  Packaging: Many boxes are prism-shaped (rectangular prisms).

•  Crystals: Natural minerals often form prism-like shapes.

 

Solved Examples

Example 1:

Find the volume of a rectangular prism with length = 5 cm, width = 3 cm, and height = 4 cm.

Ans: Volume = 5 × 3 × 4 = 60 cm³  

Example 2:

 A triangular prism has a base triangle with base = 6 cm and height = 4 cm. The prism’s height is 10 cm.

Ans: Volume = (½ × 6 × 4) × 10 = 12 × 10 = 120 cm³  

Example 3:

What is the surface area of a rectangular prism with l = 4 cm, w = 2 cm, and h = 3 cm?

Ans: SA = 2(lw + lh + wh) = 2(8 + 12 + 6) = 2 × 26 = 52 cm²  

Example 4:

Identify whether a slanted box is a right prism or an oblique prism.

Ans: Since it is slanted, it is an oblique prism

Example 5:

 A pentagonal prism has a base area of 30 cm² and a height of 8 cm. Find the volume.

Ans: Volume = 30 × 8 = 240 cm³  

These problems reinforce your understanding of the volume of prisms, types, and real-world problem-solving.

 

FAQs on Prism

1. What is called a prism?

Answer: A prism is a 3D solid object with two identical polygonal bases and flat rectangular faces joining the corresponding sides.

2. What is the prism formula?

Answer: The volume of a prism = Base Area × Height. Surface Area = 2 × Base Area + Perimeter of Base × Height.

3. How to calculate a prism?

Answer: To calculate the volume, multiply the area of the base by the height. For surface area, calculate the area of all faces and add them.

4. What is the law of a prism?

Answer: In optics, the prism law relates the deviation angle of light through a prism to its angle and refractive index:
δ = (n - 1) × A,
Where δ is the deviation, n is the refractive index, and A is the prism angle.