NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes

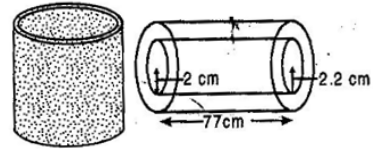
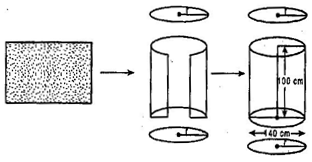
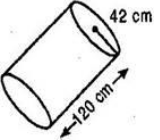
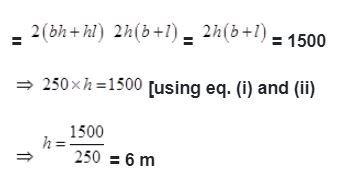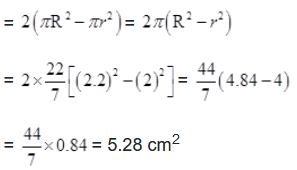Given: Length of bigger cardboard box (L) = 25 cm

Breadth (B) = 20 cm and Height (H) = 5cm

 

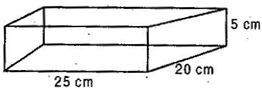
Total surface area of bigger cardboard box

= 2 (LB + BH + HL)

= 2 (25 x 20 + 20 x 5 + 5 x 25)

= 2 (500 + 100 + 125)

= 1450 cm2

5% extra surface of total surface area is required for all the overlaps.

5% of 1450 = 5/100*1450= 72.5 cm2

Now, total surface area of bigger cardboard box with extra overlaps

= 1450 + 72.5 = 1522.5 cm2

Total surface area with extra overlaps of 250 such boxes

= 250 x 1522.5 = 380625 cm2

Since, Cost of the cardboard for 1000 cm2 = Rs. 4

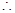Cost of the cardboard for 1cm2 = Rs. 4/1000

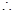Cost of the cardboard for 380625 cm2

= Rs. 4/1000*38605= Rs. 1522.50

Now length of the smaller box (l)= 15 cm,

 

 

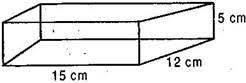
Breadth (b)= 12 cm and Height (h)= 5 cm

Total surface area of the smaller cardboard box

= 2(lb+bh+hl)

= 2 (15 x 12 + 12 x 5 + 5 x 15)

= 2 (180 + 60 +75) = 2 x 315 = 630 cm2

5% of extra surface of total surface area is required for all the overlaps.

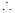5% of 630 = 5*100*630= 31.5 cm2

Total surface area with extra overlaps = 630 + 31.5 = 661.5 cm2

Now Total surface area with extra overlaps of 250 such smaller boxes

= 661.5 x 250 = 165375 cm2

Cost of the cardboard for 1000 cm2 = Rs. 4

Cost of the cardboard for 1cm2 = Rs. 4/1000

Cost of the cardboard for 165375 cm2 = Rs. 4/1000*165375= Rs. 661.50

Total cost of the cardboard required for supplying 250 boxes of each kind

= Total cost of bigger boxes + Total cost of smaller boxes

= Rs. 1522.50 + Rs. 661.50

= Rs. 2184

 

Given: Length of the brick (l)

= 22.5 cm, Breadth (b)

= 10 cm and Height (h)= 7.5 m

Surface area of the brick

= 2(lb+bh+hl)

= 2 (22.5 x 10 + 10 x 7.5 + 7.5 x 22.5)

= 2 (225 + 75 + 468.75)

= 937.5 cm2

= 0.09375 m2 [1 cm = 0.01 m]

Now No. of bricks to be painted

total area of to be painted/area of bricks=9.375/0.09375

= 100

Hence 100 bricks can be painted.

 

Given: Length (l)= 5 m, Breadth (b)= 4 m and Height (h)= 3 m

Area of the four walls = Lateral surface area = 2(bh+hl)= 2h(b+l)

= 2 x 3 (4 + 5)

= 2 x 9 x 3 = 54 m2

Area of ceiling = = 5 x 4 = 20 m2

Total area of walls and ceiling of the room = 54 + 20 = 74 m2

Now Cost of white washing for 1 m2 = Rs. 7.50

Cost of white washing for 74 m2 = 74 x 7.50 = Rs. 555

 

Given: Perimeter of rectangular wall

= 2(l+b)= 250 m ……….(i)

Now Area of the four walls of the room

=total cost to paint wallsof the room/cost  paint to 1 m2 of the walls

=1500/10 = 1500 m2 ……….(ii)

Area of the four walls = Lateral surface area

Hence required height of the hall is 6 m.

 

(i) Which box has the greater lateral surface area and by how much?

(ii) Which box has the smaller total surface area and how much?

Solution:
(i) Lateral surface area of a cube = 4 (side)2 = 4 x (10)2 = 400 cm2

Lateral surface area of a cuboid = 2h(b+l)

= 2 x 8 (12.5 + 10) = 16 x 22.5 = 360 cm2

Lateral surface area of cubical box is greater by (400 – 360) = 40 cm2

(ii) Total surface area of a cube = 6 (side)2

= 6 x (10)2 = 600 cm2

Total surface area of cuboid = 2h(lb+bh+hl)

= 2 (12.5 x 10 + 10 x 8 + 8 x 12.5)

= 2 (125 + 80 + 100)

= 2 x 305 = 610 cm2

Total surface area of cuboid box is greater by (610 – 600) = 10 cm2

 

(i) The area of the sheet required for making the box.

(ii) The cost of sheet for it, if a sheet measuring 1m2 cost Rs.20.

Solution:
(i) Given: Length (l)= 1.5 m, Breadth (b)= 1.25 m and Depth (h)

= 65 cm = 0.65 m

Area of the sheet required for making the box open at the top =2(bh+hl)+lb

= 2(1.25*0.65+*1.5)+1.5*1.25

= 2(0.8125+0.975)+1.875

= 2*1.7875+1.875

= 3.575 + 1.875 = 5.45 m2

(ii) Since, Cost of 1 m2 sheet = Rs. 20

Cost of 5.45 m2 sheet = 20 x 5.45 = Rs. 109

Given: Length of base (l)= 4 m, Breadth (b)

= 3 m and Height (h)= 2.5 m

Tarpaulin required to make shelter

= Surface area of 4 walls + Area of roof

= 2h(l+b)+lb

= 2 (4 + 3) 2.5 + 4 x 3

= 35 + 12 = 47 m2

Hence 47 m2 of the tarpaulin is required to make the shelter for the car.

 

(i) Given: Length of glass herbarium (l)= 30 cm,

Breadth (b)= 25 cm and Height (h)= 25 m

 

 

Total surface area of the glass

= 2(lb+bh+hl)

= 2 (30 x 25 + 25 x 25 + 25 x 30)

= 2 (750 + 625 + 750)

= 2 x 2125 = 4250 cm2

Hence 4250 cm2 of the glass is required to make a herbarium.

(ii) Tape is used at 12 edges.

Tape is used at 4 lengths, 4 breadths and 4 heights.

Total length of the tape = 4(l+b+hl)

= 2 (30 + 25 + 25) = 320 cm

Hence 320 cm of the tape if needed to fix 12 edges of herbarium.

 

 

(i) Length of the pipe = 77 cm, Inner diameter of cross-section = 4 cm

Inner radius of cross-section = 2 cm

Inner curved surface area of pipe = 2πrh=2 * 22/7 * 2 * 77

= 2 x 22 x 2 x 11 = 968 cm2

(ii) Length of pipe = 77 cm, Outer diameter of pipe = 4.4 cm

Outer radius of the pipe = 2.2 cm

Outer surface area of the pipe =2πrh

=2 * 22/7 * 2 * 77

= 44 x 2.2 x 11 = 1064.8 cm2

(iii) Now there are two circles of radii 2 cm and 2.2 cm at both the ends of the pipe.

Area of two edges of the pipe = 2 (Area of outer circle – area of inner circle)

 

= 5.28 cm2

Total surface area of pipe

= Inner curved surface area + Outer curved surface area + Area of two edges

= 968 + 1064.8 + 5.28 = 2038.08 cm2

Diameter of pillar = 50 cm

Diameter of roller = 84 cm

 

Given: Height of cylinder (h)= 14 cm, Curved Surface Area = 88 cm2

Let radius of base of right circular cylinder = r cm

 

Diameter of the base of the cylinder = 2r= 2 x 1 = 2 c=>m

 

Curved surface area of the cylinder

= 4.4 m2, Radius of cylinder = 0.7 m

Let height of the cylinder = h

 

Given: Diameter = 140 cm

  

Hence 7.48 m2 metal sheet is required to make the close cylindrical tank.

The length (height) of the cylindrical pipe = 28 m

Diameter = 5 cm

Radius = 5/2 cm

Curved surface area of the pipe =2πrh

(i) Diameter of cylindrical petrol tank = 4.2 m

Radius of the cylindrical petrol tank

= 4.2/2= 2.1 m

And Height of the tank = 4.5 m

Curved surface area of the cylindrical tank =2πrh

 

Radius of a cylindrical pen holder (r)= 3 cm

Height of the cylindrical pen holder (h)

= 10.5 cm

Cardboard required for pen holder = CSA of pen holder + Area of circular base

Height of each of the folding at the top and bottom (h)= 2.5 cm

Height of the frame (H) = 30 cm

Diameter = 20 cm

Radius = 10 cm

Now cloth required for covering the lampshade

= CSA of top part + CSA of middle part + CSA of bottom part

 

= 2200 cm2

 

Slant height of cone (l)= 21 m

Diameter of cone = 24 m

Radius of cone (r)= 24/2= 12 m

Total surface area of cone = πr(l + r)

=

= = 1244.57 m2

 

(i) Slant height of cone (l)= 14 cm

Curved surface area of cone = 308 cm2

πrl= 308

(ii) Total surface area of the cone

= Curved surface area + Area of circular base

 

= 462 cm2

Height of the conical tent()= 10 m

Radius of the conical tent (r)= 24 m

(i) Slant height of the tent

 

(ii) Canvas required to make the tent

= Curved surface area of the tent= πrl

= = m2

Cost of 1 m2 canvas = Rs. 70

Cost of m2 canvas

= 70 x = Rs. 137280

 

Height of the conical tent ()= 8 m and Radius of the conical tent (r)= 6 m

Slant height of the tent

Area of tarpaulin = Curved surface area of tent = πrl= 3.14 x 6 x 10 = 188.4 m2

Width of tarpaulin = 3 m

Let Length of tarpaulin = L

Area of tarpaulin = Length x Breadth

= L x 3 = 3L

Now According to question,

3L = 188.4

L = = 62.8 m

The extra length of the material required for stitching margins and cutting is 20 cm = 0.2 m.

So the total length of tarpaulin bought is (62.8 + 0.2) m = 63 m

 

Slant height of conical tomb (l)

= 25 m, Diameter of tomb = 14 m

Radius of the tomb (r) = 14/2 = 7 m

Curved surface are of tomb = πrl

= = 550 m2

Cost of white washing 100 m2

= Rs. 210

So, Cost of white washing 1 m2 =

So, Cost of white washing 550 m2

= = Rs. 1155

 

Diameter = 10.5 cm

Radius (r)= 10.5/2= 21/4cm

Slant height of cone (l)= 10 cm

Curved surface area of cone= πr(l + r)

= = 165 cm2

Total surface area of cone = πr(l + r)

=

= = 251.625 cm2

 

Radius of cap (r)= 7 cm,

Height of cap () = 24 cm

Slant height of the cone

= 25 cm

Area of sheet required to make a cap

= CSA of cone = πrl

= = 550 cm2

Area of sheet required to make 10 caps = 10 x 550 = 5500 cm2

Diameter of cone = 40 cm

Radius of cone (r)=40/2 = 20 cm

= 20/100 m = 0.2 m

Height of cone ()= 1 m

Slant height of cone

= m

Curved surface area of cone =

= 3.14 x 0.2 x

= 0.64056 m2

Cost of painting 1 m2 of a cone

= Rs. 12

Cost of painting 0.64056 m2 of a cone

= 12 x 0.64056= Rs. 7.68672

Cost of painting of 50 such cones

= 50 x 7.68672 = Rs. 384.34 (approx.)

(i) Radius of sphere = 105 cm

Surface area of sphere = 4πr2

= = 1386 cm2

(ii) Radius of sphere = 5.6 m

Surface area of sphere = 4πr2

= = 3.94.84 m2

(iii) Radius of sphere = 14 cm

Surface area of sphere = 4πr2

= = 2464 cm2

(i) Diameter of sphere = 14 cm,

Therefore Radius of sphere = 14/2 = 7 cm

Surface area of sphere = 4πr2

= = 616 cm2

(ii) Diameter of sphere = 21 cm

Radius of sphere = 21/2 cm

Surface area of sphere = 4πr2

= = 1386 cm2

(iii) Diameter of sphere = 3.5 cm

Radius of sphere = 3.5/2 = 1.75 cm

Surface area of sphere = 4πr2

= = 38.5 cm2

 

Radius of hemisphere (r) = 10 cm

Total surface area of hemisphere = 3πr2

= 3 x 3.14 x 10 x 10 = 942 cm2

Hence total surface area of hemisphere is

942 cm2

 

(i) Radius of sphere = r

Surface area of sphere

= 2π(radius)2 = 2πr2

The cylinder just encloses the sphere in it.

The height of cylinder will be equal to diameter of sphere.

And The radius of cylinder will be equal to radius of sphere.

(ii) Curved surface area of cylinder

= 2πrh= 2πr x πr

= 4πr2

 

So, Required ratio = 1 :1

 

I case: Radius of balloon (r) = 7 cm

Surface area of balloon = 4πr2

=4π x 7 x 7 cm2……….(i)

II case: Radius of balloon (R) = 14 cm

Surface area of balloon = 4πr2

= 4π x 14 x 14 cm2 …….(ii)

Now, Ratio [from eq. (i) and (ii)],

Hence, required ratio = 1 : 4

Inner diameter of bowl

= 10.5 cm

Inner radius of bowl (r) = 10.5/2

= 5.25 cm

Now, Inner surface area of bowl

= 2πr2

=

Cost of tin-plating per 100 cm2

= Rs. 16

Cost of tin-plating per 1 cm2 =

Cost of tin-plating per cm2

= = Rs. 27.72

 

Let diameter of Earth =

Radius of Earth (r) =

Surface area of Earth = 4πr2

=

Now, Diameter of Moon = of diameter of Earth =

Radius of Moon (r) =

Surface area of Moon = 4πr2

=

Now, Ratio =

=

Required ratio = 1 : 16

 

Surface area of sphere = 154 cm2

4πr2= 154

 

Inner radius of bowl (r) = 5 cm

Thickness of steel (t) = 0.25 cm

Outer radius of bowl (R) = r + t

= 5 +0.25 = 5.25 cm

Outer curved surface area of bowl

 

= 173.25 cm2

 

Volume of one cuboidal brick

= l x b x h

= 22.5 cm x 11. 5 cm x 7.5 cm3

= 1940.625 cm3

= 0.001940625 m3

Volume of cuboidal wal

= 10 m x 6 m x 1.5 m= 90 m3

Minimum number of bricks required

 

= 46377 [Since bricks cannot be in fraction]

 

Given: Length (l)= 4 cm, Breadth (b) = 2.5 cm, Height (h) = 1.5 cm

Volume of a matchbox = l x b x h

= 4 x 2.5 x 1.5

= 15 cm3

Volume of a packet containing 12

such matchboxes = 12 x 15 = 180 cm3

 

Volume of water in cuboidal tank = 6 m x 5 m x 4.5 m

= 135 m3= 135 x 1000 liters

= 135000 liters

Hence tank can hold 135000 liters of water.

 

Let height of cuboidal vessel = m

Volume of liquid in cuboidal vessel

= 380 m3

= 380 cm3

=> 10 m x 8 m x = 380

=> = = 4.75 m

Hence cuboidal vessel is 4.75 m high.

 

Capacity of cuboidal tank

= 50000 liters

= 50000 liters

2.5 m x b x 10 m = m3

Hence breadth of cuboidal tank is 2 m.

 

Volume of cuboidal pit = 8 m x 6 m x 3 m= 144 m3

Cost of digging 1 m3 cuboidal pit

= Rs. 30

Cost of digging 144 m3 cuboidal pit

= 30 x 144 = Rs. 4320

 

Capacity of cuboidal tank

 = 20 m x 15 m x 6 m

= 1800 m3 = 1800 x 1000 liters

 

= 1800000 liters

Water required by her head per day

= 150 liters

Water required by 4000 persons per day = 150 x 4000 = 600000 liters

Number of days the water will last

=

= = 3

Hence water of the given tank will last for 3 days.

 

Capacity of cuboidal godown

= 40 m x 25 m x 15 m = 15000 m3

Capacity of wooden crate = 1.5 m x 1.25 m x 0.5 m = 0.9375 m3

Maximum number of crates that can be stored in the godown

=

=  = 16000

Hence maximum 16000 crates can be stored in the godown.

 

Volume of solid cube = (side)3

= (12)3 = 1728 cm3

According to question, Volume of each new cube= 1/8 (Volume of original cube)

= = 216 cm3

Side of new cube = = 6 cm

Now, Surface area of original solid cube = 6 (side)2

= 6 x 12 x 12 = 864 cm2

Now, Surface area of original solid cube = 6 (side)2= 6 x 6 x 6 = 216 cm2

Now according to the question,

 

Hence required ration between surface area of original cube to that of new cube = 4 : 1.

 

Since water flows at the rate of 2 km per hour, the water from 2 km of the river flows into the sea in one hour.

Therefore, the volume of water flowing into the sea in one hour

= Volume of a cuboid

= = 2000 m x 40 m x 3 m

= 240000 m3 [1 km = 1000 m]

Now, Volume of water flowing into sea in 1 hour (in 60 minutes)

= 240000 m3

Volume of water flowing into sea in 1 minute = = 4000 m3

 

Given: Volume of wooden plank

= 0.25 m3

=> lx 2.5 x 0.025 = 0.25

l = 4 m

Hence required length of wooden plank is 4 m.

 

 

 

Radius of drum (r) = 4.2 m and Height of drum ()= 5 m

 

Volume of a drum = πr2h

=

= 22 x 0.6 x 4.2 x 5 = 277.2 m3

Now, Number of bags

=

= = 99

Hence 99 bags are needed to fill the drum.

 

Diameter of graphite = 1 mm

Radius of drum = 0.5 mm

= 0.05 cm

 

Height of graphite ()= 14 cm

Volume of graphite = πr2h

= = 0.11 cm3

Diameter of pencil = 7 mm

Radius of pencil (R) = 3.5 mm

= 0.35 cm

Volume of pencil=

= = 5.39 cm3

Now, Volume of wood = Volume of pencil – Volume of graphite

= 5.39 – 0.11 = 5.28 cm3

 

Diameter of circular base of cylindrical bowl = 7 cm

 

Radius of circular base of cylindrical

bowl (r)= 7/2 cm

Height of the bowl ()= 4 cm

Now, Volume of cylindrical bowl = πr2h

= = 22 x 7 = 154 cm3

Quantity of soup filled in a bowl

= 154 cm3

Therefore, total quantity of soup to be prepared by the hospital = 250 x 154

= 38500 cm3

= liter [1 liter = 1000 cm3]

= 38.5 liters

 

I case: Length of tin = 5 cm, Width of tin (b)= 4 cm

and Height of tin (h) = 15 cm

Then, Capacity of tin =  = 5 x 4 x 15 = 300 cm3

II case: Diameter of base of cylinder = 7 cm

 

Radius of base of cylinder (r) = 7/2 cm

Height of cylinder = 10 cm

Capacity of cylinder =

=   = 385 cm3

From the cases I and II, we observed that

cylindrical container has greater capacity

by (385 – 300) = 85 cm3.

 

(i) inner curved surface area of the vessel.

(ii) radius of the base.

(iii) capacity of the vessel.

Solution:
v Total cost to paint inner curved surface area of the vessel = Rs. 2200

Rate = Rs. 20 per square meter

(i) Inner curved surface area of vessel =

= 110 m2

(ii) Depth of the vessel ()= 10 m

Now, Inner surface area of vessel

= 110 m2

= 110

 

= 1.75 m

(iii) Since r = 1.75 m and

= 10 m

Capacity of vessel

= Volume of cylinder = πr2h

= = 96.25 m3

= 96.25 kl [1 m3 = 1 kl]

 

Height of the vessel ()= 1 m

Capacity of vessel = 15.4 liters

= kilo liters

= 0.0154 m3 [1 m3 = 1 kl]

=> πr2h = 0.0154

 

=> r2 = 0.0007 x 7 = 0.0048

=> r = 0.07 m

Now, Area of metal sheet required = TSA of cylindrical vessel

 

= 0.4708 m2

 

Inner diameter of pipe = 28 cm

Inner radius of pipe (r)

= 24/2 = 12 cm

And Outer diameter of pipe = 28 cm

Outer radius of pipe (R)

= 28/2 = 14 m

Length of pipe (l)= 35 cm

 

Volume of wood = Volume of outer cylinder – Volume of inner cylinder

 

= 110 [ 196 – 144 ] = 110 x 52

= 5720 cm3

Weight of 1 cm3 of wood = 0.6 g

Weight of 5720 cm3 of wood

= 0.6 x 5720 = 3432 g = 3.432 kg

 

Height of the cylinder = 5 cm

Lateral surface area of the cylinder

= 94.2 cm2

=> 2πrh = 94.2

=> 2 x 3.14 x r x 5 = 94.2

= 3 cm

Volume of cylinder = πr2h

= 3.14 x 3 x 3 x 5 = 141.3 cm3

 

Height of vessel = h= 25 cm

Circumference of base of vessel

= 132 cm

=>2πr = 132

= 21 cm

Now, Volume of cylindrical vessel

= = = 34650 cm3

= liters [1000 cm3 = 1 liter]

= 34.65 liters

 

Radius (r) of heap

Height (h) of heap = 3 m

Volume of heap

=

Therefore, the volume of the heap of wheat is 86.625 m3.

Area of canvas required = CSA of cone

 

Therefore, 99.825 m2canvas will be required to protect the heap from rain.

 

(i) Given: r = 7 cm, l = 25 cm

= 24 cm

Capacity of conical vessel =

= = 1232 cm3

= 1.232 liters [1000 cm3= 1liter]

 

(ii) Given: = 12 cm, l = 13 cm

 

= 5 cm

Capacity of conical vessel =

= = cm3

= liters

[1000 cm3= 1liter]

= liter

 

(i) Given: r = 6 cm, = 7 cm

Volume of cone =

=

= 264 cm3

(ii) Given: r= 3.5 cm, = 12 cm

Volume of cone =

=

= 154 cm3

Height of the cone = 15 cm

Volume of cone = 1570 cm3

= 1570

= 10 cm

Hence required radius of the base is 10 cm.

 

Height of the cone ()= 9 cm

 

Volume of cone = 48π cm3

r = 4 cm

Diameter of base = 2r = 2 x 4 = 8 cm

 

Diameter of pit = 3.5 m

Radius of pit (r)= 3.5/2 = 1.75 m

Depth of pit = 12 m

Capacity of pit =

 

= m3 = 35.8 m3

= 38.5 kl [1 m3 = 1 kl]

 

(i) Diameter of cone = 28 cm

Radius of cone = 14 cm

Volume of cone = 9856 cm3

= 9856

 

= 48 cm

(ii) Slant height of cone =

 

= 50 cm

(iii) Curved surface area of cone = πrl = = 2200 cm2

When right angled triangle ABC is revolved about side 12 cm, then the solid formed is a cone.

In that cone, Height () = 12 cm

And radius (r) = 5 cm

Therefore, Volume of cone =

=

= 100π cm3

 

When right angled triangle ABC is revolved about side 5 cm, then the solid formed is a cone.

In that cone, Height ()= 5 cm

And radius ( r )= 12 cm

Therefore, Volume of cone =

=

= 240π cm3

Now,

=

Required ratio = 5 : 12

 

Since, diameter of the largest right circular cone that can be fitted in a cube = Edge of cube

2r = 14 cm

r = 7 cm

And also Height of the cone = Edge of cube = 14 cm

Now, Volume of the largest cone

=

 

= 718.66 cm3

 

Diameter of hemispherical bowl

= 10.5 cm

Radius of hemispherical bowl ( r )

= = 5.25 cm

Volume of milk in hemispherical bowl

 

= 0.303187 liters

= 0.303 liters (approx.)

 

Inner radius of hemispherical tank ( r ) = 1 m = 100 cm

Thickness of sheet = 1 cm

Outer radius of hemispherical tank (R) = 100 + 1 = 101 cm

Volume of iron of hemisphere

 

= 63487.81 cm3

= 0.06348 m3

 

Surface area of sphere = 154 cm2

4πr2 = 154

Now, Volume of sphere

 

 

Cost of white washing from inside = Rs. 498.96

Rate of white washing = Rs. 2

Area white washed

= = 249.48 cm2

Inside surface area of the dome

= 249.48 cm2

2πr2 = 249.48

 

= 5.67 x 7

r = 6.3

So, Volume of the dome

=

= 523.9 cm3

 

(i) Let radius of sphere be r and radius of new sphere be R.

27 x Volume of sphere = Volume of new sphere

27 x =

 

 

Diameter of spherical capsule = 3.5 mm

 

Radius of spherical capsule ( r )

= mm

Medicine needed to fill the capsule

= Volume of sphere =

 

= 22.46 mm3 (Approx.)

 

 

 

Diameter of metallic ball = 4.2 cm

Radius of metallic ball (r)= 4.2/2

= 2.1 cm

Volume of metallic ball =

 

= 38.808 cm3

Density of metal = 8.9 g per cm3

Mass of 1 cm3 = 8.9 g

Mass of 38.808 cm3 = 8.9 x 38.808

= 345.3912 g = 345.39 g (approx).

 

(i) Diameter of spherical ball

= 28 cm

Radius of spherical ball ( r) = 28/2

= 14 cm

According to question, Volume of water replaced = Volume of spherical ball

=

=

= cm3

(ii) Diameter of spherical ball = 0.21 m

Radius of spherical ball (r)= 0.21/2m

According to question,

Volume of water replaced = Volume of spherical ball

=

 

= 0.004851 m3

 

Let diameter of earth be x

Radius of earth (r) = x/2

Now, Volume of earth =

[Earth is considered to be a sphere]

= ……..(i)

According to question,

Diameter of moon = x Diameter of earth=

Radius of moon (R) =

Now, Volume of Moon =

[Moon is considered to be a sphere]

 

[From eq. (i)]

So, Volume of moon is the volume of earth.

 

Radius of sphere ( r )= 7 cm

Volume of sphere =

=

= cm3

(ii) Radius of sphere ( r )= 0.63 m

Volume of sphere =

 

= 1.047816 m3 = 1.05 m3 (approx.)

 

External faces to be polished

= Area of six faces of cuboidal bookshelf – 3 (Area of open portion ABCD)

= 2 (110 x 25 + 25 x 85 + 85 x 110) – 3 (75 x 30)

[AB = 85 – 5 – 5 = 75 cm and AD

= [⅓ x 110 – 5 – 5 – 5 – 5 = 30 cm]   

= 2 (2750 + 2125 + 9350) – 3 x 2250

= 2 x 14225 – 6750

= 28450 – 6750

= 21700 cm2

Now, cost of painting outer faces of wodden bookshelf at the rate of 20 paise.

= Rs. 0.20 per cm2 = Rs. 0.20 x 21700 = Rs. 4340

Here, three equal five sides inner faces.

Therefore total surface area

= 3 [ 2 (30 + 75) 20 + 30 x 75] [Depth = 25 – 5 = 20 cm]

= 3 [ 2 x 105 x 20 + 2250] = 3

[ 4200 + 2250]

= 3 x 6450 = 19350 cm2

Now, cost of painting inner faces at the rate of 10 paise i.e. Rs. 0.10 per cm2.

= Rs. 0.10 x 19350 = Rs. 1935

Total expenses required = Rs. 4340 + Rs. 1935 = Rs. 6275

 

Diameter of a wooden sphere

= 21 cm.

Radius of wooden sphere ( R )

= 21/2 cm

And Radius of the cylinder ( r )

= 1.5 cm

Surface area of silver painted part

= Surface area of sphere – Upper part of cylinder for support

 

= 1378.928 cm2

Surface area of such type of 8 spherical part = 8 x 1378.928

= 11031.424 cm2

Cost of silver paint over 1 cm2

= Rs. 0.25

Cost of silver paint over 11031.928 cm2 = 0.25 x 11031.928

= Rs. 2757.85

Now, curved surface area of a cylindrical support = 2πrh

= = 66 cm2

Curved surface area of 8 such cylindrical supports = 66 x 8 = 528 cm2

Cost of black paint over 1 cm2 of cylindrical support = Rs. 0.50

Cost of black paint over 528 cm2 of cylindrical support = 0.50 x 528

= Rs. 26.40

Total cost of paint required

= Rs. 2757.85 + Rs. 26.4

= Rs. 2784.25

 

Diameter of original sphere

= D = 2R

R = D/2

Curved surface area of original sphere =

According to the question,

Decreased diameter = 25% of D

=

Diameter of new sphere =

Radius of new sphere =

Now, curved surface area of new sphere =

Change in curved surface area

 

Percent change in the curved surface area

 

 

Diameter of base of conical cap

= 10 cm

 

Radius of conical cap ( r )= 5 cm

Slant height of cone 

 

= 13 cm

Curved surface area of a cap

= πrl = 3.14 x 5 x 13 = 204.1 cm2

Curved surface area of 15 caps

= 15 x 204.1 = 3061.5 cm2

Area of a sheet of paper used for making caps = 25 x 40 = 1000 cm2

82% of sheet is used after cutting

= 82% of 1000 cm2

= 820 cm2

Number of sheet = = 3.73

Hence 4 sheets area needed .