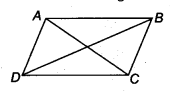
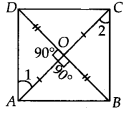
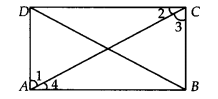
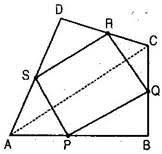
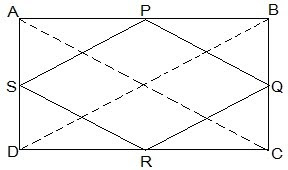
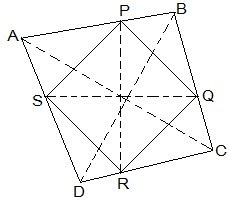
Given: P, Q, R and S are the mid-points of respective sides AB, BC, CD and DA of rhombus. PQ, QR, RS and SP are joined.
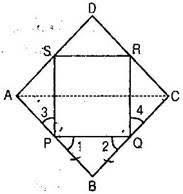
To prove: PQRS is a rectangle.
Construction: Join A and C.
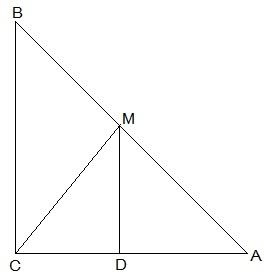
Proof: In  ABC, P is the mid-point of AB and Q is the mid-point of BC.
ABC, P is the mid-point of AB and Q is the mid-point of BC.
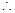 PQ
PQ  AC and PQ =
AC and PQ = 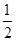 AC ……….(i)
AC ……….(i)
In 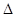 ADC, R is the mid-point of CD and S is the mid-point of AD.
ADC, R is the mid-point of CD and S is the mid-point of AD.
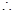 SR
SR  AC and SR =
AC and SR = 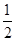 AC ……….(ii)
AC ……….(ii)
From eq. (i) and (ii), PQ  SR and PQ = SR
SR and PQ = SR
 PQRS is a parallelogram.
PQRS is a parallelogram.
Now ABCD is a rhombus. [Given]
 AB = BC
AB = BC
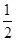 AB =
AB = 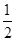 BC
BC  PB = BQ
PB = BQ
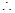
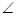 1 =
1 = 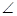 2 [Angles opposite to equal sides are equal]
2 [Angles opposite to equal sides are equal]
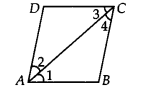
Now in triangles APS and CQR, we have,
AP = CQ [P and Q are the mid-points of AB and BC and AB = BC]
Similarly, AS = CR and PS = QR [Opposite sides of a parallelogram]
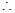
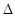 APS
APS 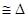 CQR [By SSS congreuancy]
CQR [By SSS congreuancy]
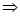
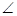 3 =
3 = 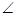 4 [By C.P.C.T.]
4 [By C.P.C.T.]
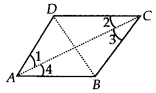
Now we have 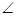 1 +
1 + 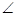 SPQ +
SPQ + 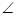 3 =
3 = 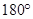
And 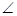 2 +
2 + 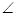 PQR +
PQR + 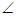 4 =
4 = 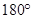 [Linear pairs]
[Linear pairs]
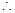
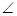 1 +
1 + 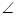 SPQ +
SPQ + 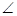 3 =
3 = 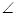 2 +
2 + 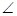 PQR +
PQR + 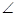 4
4
Since 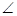 1 =
1 = 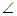 2 and
2 and 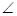 3 =
3 = 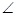 4 [Proved above]
4 [Proved above]
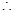
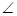 SPQ =
SPQ = 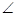 PQR ……….(iii)
PQR ……….(iii)
Now PQRS is a parallelogram [Proved above]
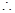
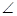 SPQ +
SPQ + 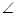 PQR =
PQR = 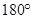 ……….(iv) [Interior angles]
……….(iv) [Interior angles]
Using eq. (iii) and (iv),
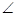 SPQ +
SPQ + 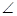 SPQ =
SPQ = 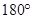
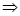 2
2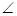 SPQ =
SPQ = 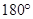
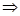
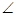 SPQ =
SPQ = 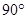
Hence PQRS is a rectangle.