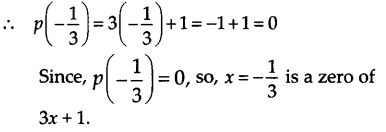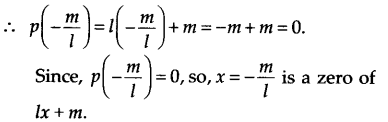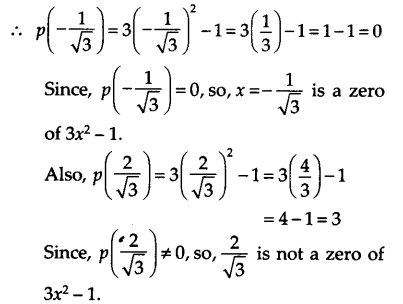(i) x+1
We need to find the zero of the polynomial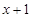 .
.
x+1=0 => x = -1
While applying the remainder theorem, we need to put the zero of the polynomial x+1 in the polynomial x3+3x2+3x+1, to get
p(x) = x3+3x2+3x+1
p(0)
= -1+3-3+1
= 0
Therefore, we conclude that on dividing the polynomial x3+3x2+3x+1 by x+1, we will get the remainder as 0.
(ii)x=-1/2
We need to find the zero of the polynomial x-1/2.
x-1/2 = 0 => x = 1/2
While applying the remainder theorem, we need to put the zero of the polynomial x-1/2 in the polynomial x3+3x2+3x+1, to get
p(x) = x3+3x2+3x+1
= p(1/2) = (1/2)3 + 3(1/2)2 + 3(1/2) + 1
= 1/8 + 3(1/4) + 3/2 +1
= 1+6+12+8/8
= 27/8
Therefore, we conclude that on dividing the polynomial x3+3x2+3x+1 by x-1/2 , we will get the remainder as 27/8.
(iii)
We need to find the zero of the polynomial x.
x=0
While applying the remainder theorem, we need to put the zero of the polynomial x in the polynomial x3+3x2+3x+1, to get
p(x) = x3+3x2+3x+1
= p(0) = (0)3 + 3(0)2 + 3(0) +1
=0+0+0+1
=1
Therefore, we conclude that on dividing the polynomial x3+3x2+3x+1 by x, we will get the remainder as 1.
(iv)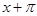
We need to find the zero of the polynomial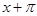 .
.

While applying the remainder theorem, we need to put the zero of the polynomial 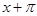 in the polynomial x3+3x2+3x+1, to get
in the polynomial x3+3x2+3x+1, to get
p(x) = x3+3x2+3x+1
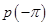
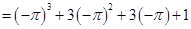
= 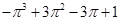
Therefore, we conclude that on dividing the polynomial x3+3x2+3x+1 by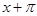 , we will get the remainder as
, we will get the remainder as 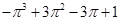 .
.
(v) 5+2x
We need to find the zero of the polynomial 5+2x.
5+2x = 0 => x = - 5/2
While applying the remainder theorem, we need to put the zero of the polynomial 5+2x in the polynomial x3+3x2+3x+1, to get
p(x) = x3+3x2+3x+1
p(-5/2) = (-5/2)3 + 3(-5/2)2 + 3(-5/2) +1
= -125/8 + 3(25/4) - 15/2 + 1
= -125/8 + 75/4 - 15/2 + 1
= -125 + 150 - 60 + 8 / 8
= -27/4
Therefore, we conclude that on dividing the polynomial x3+3x2+3x+1 by 5+2x, we will get the remainder as -27/4.

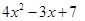
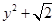
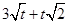
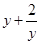
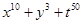
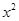 in each of the following :
in each of the following :