NCERT Solutions for Class 9 Maths Chapter 12 Statistics

  Some examples of data that we can gather from our day to day life are:

(i) Number of students in our class.

(ii) Number of fans in our school.

(iii) Electricity bills of our house for last two years.

(iv) Election results obtained from television or newspapers.

(v) Literacy rate figures obtained from Educational Survey.

(vi) Heights of 20 students of our class.

(vii) Maximum temperatures of the days of a particular week from television.

(viii) Number of members in the families of your locality from a record.

(ix) Distances from the school of the homes of ten students.

Primary data: When the information was collected by the investigator herself or himself with a definite objective in her or his mind, the data obtained is called Primary data. These types of data are original in character and collected for the first time for their own use.

Above mentioned (i), (ii), (iii), (iv) and (ix) are the examples of primary data.

Secondary data: When the information was gathered from a source (like newspapers, television or some records) which already had the information stored is called Secondary data. Such data has been collected by someone else in another context needs to be used with great care. These data are collected for a purpose other than that of original investigator.

Above mentioned (iv), (v), (vii) and (viii) are the examples of secondary data.

It can be observed that 9 students have their blood group as A, 6 as B, 3 as AB, and 12 as O.

Therefore, the blood group of 30 students of the class can be represented as follows.

It can be observed clearly that the most common blood group and the rarest blood group among these students is O and AB respectively as 12 (maximum number of students) have their blood group as O, and 3 (minimum number of students) have their blood group as AB.

The grouped frequency distribution table for the given data is as follows:

From the table we observe that out of 40 female engineers 36 (5 +11 + 11 + 9) engineers i.e. 90% of the total female engineers reside less than 20 km from their place of work.

(i) The grouped frequency distribution table for the given data is as follows:

(ii) From the data we observe that relative humidity is high. So data appears to be taken in the rainy season.

(iii) From the data, we observe that

Highest relative humidity = 99.2%

Lowest relative humidity = 84.9%

Range = (99.2 – 84.9)% = 14.3%

(i) The grouped frequency distribution table for the given data is as follows:

(ii) From the frequency distribution table drawn above, we conclude that more than 50% of the students are shorter than 165 cm.

(i) The grouped frequency distribution table for the given data is as follows:

(ii) From the above frequency distribution we observe that the concentration of Sulphur dioxide was more than 0.11 ppm for 8 days.

(i) The grouped frequency distribution table for the given data is as follows:

(a) The value of π up to 50 decimal places is given as table:

3.14159265358979323846264338327950288419716939937510

The frequency distribution table of the digits after the decimal point in the value of πis as follows:

(b) Maximum frequency is 8.

Hence 3 is the most frequently occurring digit.

Least frequency is 2.

Hence 0 is the least occurring digit.

(i) Frequency distribution table for the given data is as follows:

(ii) From the frequency table we observe that number of children in the class interval 15 – 20 is 2.

So 2 children view television for 15 hours or more than 15 hours a week.

Grouped frequency distribution table for the given data is as follows:

(i) By representing causes on x-axis and family fatality rate on y-axis and choosing an appropriate scale (1 unit = 5% for y axis), the graph of the information given above can be constructed as follows.

All the rectangle bars are of the same width and have equal spacing between them.

(ii) Reproductive health condition is the major cause of women’s ill health and death worldwide as 31.8% of women are affected by it.

(iii) The factors are as follows.

1. Lack of medical facilities

2. Lack of correct knowledge of treatment

(i) By representing section (variable) on x-axis and number of girls per thousand boys on y-axis, the graph of the information given above can be constructed by choosing an appropriate scale (1 unit = 100 girls for y-axis)

Here, all the rectangle bars are of the same length and have equal spacing in between them.

(ii) It can be observed that maximum number of girls per thousand boys (i.e., 970) is for ST and minimum number of girls per thousand boys (i.e., 910) is for urban.

Also, the number of girls per thousand boys is greater in rural areas than that in urban areas, backward districts than that in non-backward districts, SC and ST than that in non-SC/ST.

(i) By taking polling results on x-axis and seats won as y-axis and choosing an appropriate scale (1 unit = 10 seats for y-axis), the required graph of the above information can be constructed as follows.

(Here, the rectangle bars are of the same length and have equal spacing in between them.

(ii) Political party ‘A’ won maximum number of seats.

(i) It can be observed that the length of leaves is represented in a discontinuous class interval having a difference of 1 in between them. Therefore, has to be added to each upper class limit and also have to subtract 0.5 from the lower class limits so as to make the class intervals continuous.

Taking the length of leaves on x-axis and the number of leaves on y-axis, the histogram of this information can be drawn as above.

Here, 1 unit on y-axis represents 2 leaves.

(ii) Other suitable graphical representation of this data is frequency polygon.

(iii) No, as maximum number of leaves (i.e., 12) has their length in between 144.5 mm and 153.5 mm. It is not necessary that all have their lengths as 153 mm.

(i) Representation of the given in the form of histogram is as follows:

(ii) Number of lamps having lifetime of more than 700 hours = 74 + 62 +48 = 184

We can find the class marks of the given class intervals by using the following formula.

Class mark

Taking class marks on x-axis and frequency on y-axis and choosing an appropriate scale (1 unit = 3 for y-axis), the frequency polygon can be drawn as follows.

It can be observed that the performance of students of section ‘A’ is better than the students of section ‘B’ in terms of good marks.

New series of given data for plotting the frequency polygon:

Frequency polygon of team A and team B

Here the classes are not of equal size. Here minimum class is 1, therefore

The histogram using these lengths

Here the classes are not of equal size. Here minimum class is 1, therefore

The histogram using these lengths

We know that, Mean =

⇒

= = 54.8

For median,

Arrange the given data in the ascending order, we get

39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98

Here n=15 which is odd in number.

Median = term = term = 8th observation

⇒ Median = 52

⇒ Median = = 3

For mode

Here, Marks – 52 has the maximum frequency is 3. Therefore, mode = 52

We know that, Mean =

⇒ = = 2.8

For median,

Arrange the given data in the ascending order, we get

0, 1, 2, 3, 3, 3, 3, 4, 4, 5

Here n = 10 which is even in number.

∴ Median =

∴ Median = = 3

For mode

Here, Goal – 3 has the maximum frequency is 4. Therefore, mode = 3

Here number of observations = 10, which is an even number

Median =

= (5th term + 6th term)

⇒ 63 =

⇒ 63 =

⇒ 63 =

⇒ x +1

⇒ x = 62

(i) Making a frequency table, we have

Here the observation 14 has the maximum frequency 4.

Therefore, mode = 14

(ii) Making a frequency table, we have

Here the observation 7 has the maximum frequency 5.

Therefore, mode = 7

Mean = = 5083.33

Hence the mean of salary is Rs. 5083.33

(i) Mean is the suitable measure of central tendency because every term is taken in

calculation, it is effected by every item. It can further be subjected to algebraic treatment unlike other measures i.e. median and mode. As mean is rigidly defined, it is mostly used for comparing the various issues.

For example, the marks obtained by the seven students are 10, 15, 14, 18, 26, 24, 20, 14 and 27.

Mean =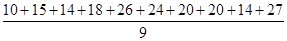

= 168/9 = 18.67

But median of 10, 15, 14, 18, 26, 24, 20, 14 and 27 is 18 and mode is 14.

From above example we conclude that mean is rigidly defined and the marks 18.67 represent the performance of 9 students, but median and mode are not so rigidly defined.

(ii) (a) Mean is much affected by the extreme value but median is not much affected by these

extremes.

For example, if there are 5 terms: 4, 7, 12, 18, 19

Mean 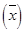is 12 in this case and median is 12.

If we add two values 450 and 1000 the new mean =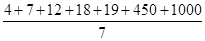

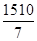= = 215.7

This is a big change as compared to the size of first five terms’ mean but new median of 4, 7, 12, 18, 19, 450, 1000 is 18 which is not so much changed as compared to the size of first five terms’ median.

So we conclude that the mean misrepresents the result if extreme values are present in the data.

(b) Sometimes mean gives impossible conclusion e.g. if there are 60, 50 and 42 students in three classes then mean number of students is 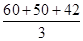= 50.67, which is impossible as students cannot be in fractions. But median of 42, 50 and 60 is 50.